全域木の判定 Bash(Beta)編（paizaランク B 相当）

問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！

問題

下記の問題をプログラミングしてみよう！

1, ..., n の番号がついた n 個の頂点とそれらをつなぐ枝からなる無向グラフを考えます。ただし、自己ループと多重辺は考えません。

隣接リストが与えられます。このとき、この隣接リストが表現するグラフが全域木ならば Yes 、そうでなければ No と出力してください。

グラフ理論における「木」とは、連結で閉路を持たない部分グラフのことを言います。ただしここで閉路とは、複数の枝が 1 つの輪になったもののことを言います。

木の特殊なものとして「全域木」があり、これはグラフの全ての頂点を含んでいる木のことを言います。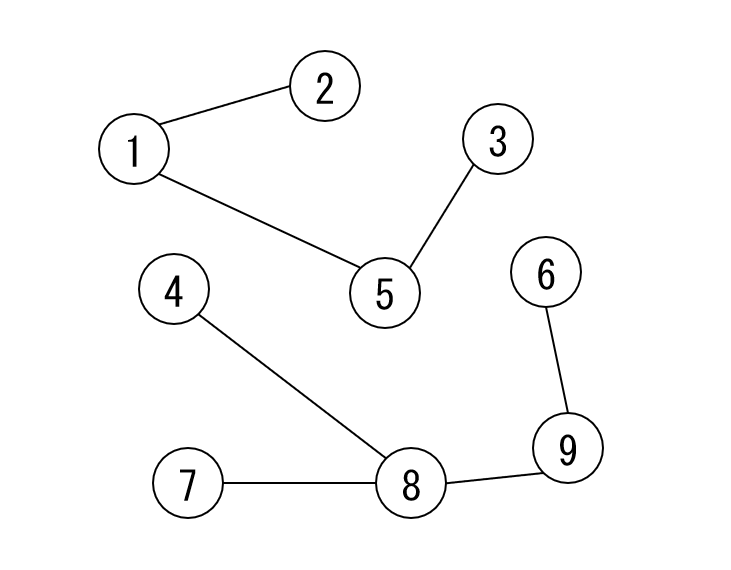

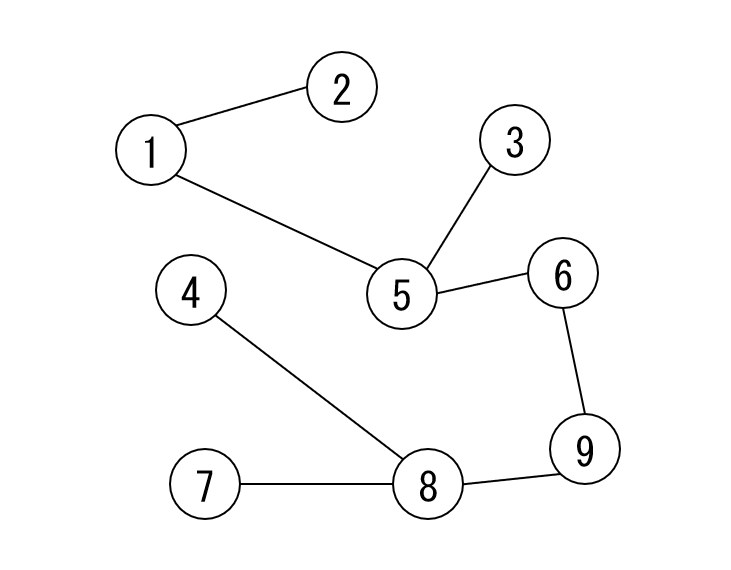
例として 9 個の頂点からなるグラフを考え、左のグラフは 2 つの木で構成されているのに対し、右のグラフは全域木となっています。

入力される値

n
v_1
a_{1,1} a_{1,2} ... a_{1,v_1}
v_2
a_{2,1} ... a_{2,v_2}
...
v_n
a_{n,1} ... a_{n,v_n}

・ 1 行目に、頂点の個数を表す整数 n が与えられます。

・ 2i 行目には頂点 i に隣接している頂点の個数が与えられ、 2i+1 行目には頂点 i に隣接している頂点の番号が半角スペース区切りで与えられます。(1 ≦ i ≦ n)

入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。標準入力からの値取得方法はこちらをご確認ください

期待する出力: 入力が全域木となっているならば Yes 、そうでなければ No と 1 行で出力してください。

条件: すべてのテストケースにおいて、以下の条件をみたします。

・ 3 ≦ n ≦ 12

・ 1 ≦ v_i ≦ n-1 (1 ≦ i ≦ n)

・ 1 ≦ i ≦ n について

・ v_i = 1 のとき : 1 ≦ a_{i,1} ≦ n

・ v_i > 1 のとき : 1 ≦ a_{i,j} < a_{i,j+1} ≦ n (1 ≦ j ≦ (v_i)-1)

入力例1: 4
2
2 3
1
1
2
1 4
1
3

出力例1: Yes

入力例2: 5
1
2
1
1
2
4 5
2
3 5
2
3 4

出力例2: No

問題一覧へ戻る