連結成分の数 VB(Beta)編（paizaランク B 相当）

問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！

問題

下記の問題をプログラミングしてみよう！

1, ..., n の番号がついた n 個の頂点とそれらをつなぐ枝からなる無向グラフを考えます。ただし、自己ループと多重辺は考えません。

隣接リストが与えられます。このとき、グラフの連結成分の数を出力してください。ただし、グラフの連結成分とは、極大で連結な部分グラフのことを意味します。例として、以下のようなグラフでは、連結成分は 4 個となります。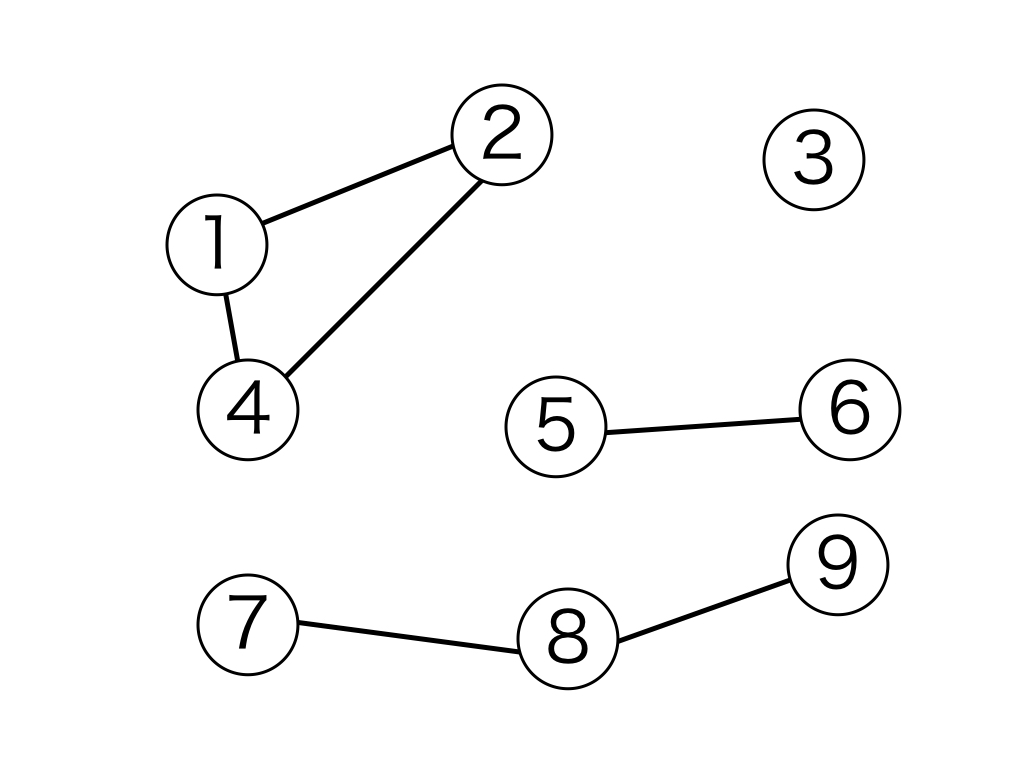

ただし、今回の問題では任意の頂点は少なくとも 1 つの頂点に隣接しているため、上の画像の3番の頂点のような一つの頂点だけからなる連結成分は存在しません。

そして連結成分の数を求めるには、

訪問済みでない頂点から深さ優先探索を行って連結成分を求め、それらを訪問済みにする

という操作を全ての頂点が訪問済みになるまで繰り返し、その繰り返した回数が連結成分の数となります。

入力される値

n
v_1
a_{1,1} a_{1,2} ... a_{1,v_1}
v_2
a_{2,1} ... a_{2,v_2}
...
v_n
a_{n,1} ... a_{n,v_n}

・ 1 行目に、頂点の個数を表す整数 n が与えられます。

・ 2i 行目には頂点 i に隣接している頂点の個数が与えられ、 2i+1 行目には頂点 i に隣接している頂点の番号が半角スペース区切りで与えられます。(1 ≦ i ≦ n)

入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。標準入力からの値取得方法はこちらをご確認ください

期待する出力: グラフの連結成分の数を 1 行で出力してください。

条件: すべてのテストケースにおいて、以下の条件をみたします。

・ 3 ≦ n ≦ 20

・ 1 ≦ v_i ≦ n-1 (1 ≦ i ≦ n)

・ 1 ≦ i ≦ n について

・ v_i = 1 のとき : 1 ≦ a_{i,1} ≦ n

・ v_i > 1 のとき : 1 ≦ a_{i,j} < a_{i,j+1} ≦ n (1 ≦ j ≦ (v_i)-1)

入力例1: 3
2
2 3
2
1 3
2
1 2

出力例1: 1

入力例2: 5
1
2
1
1
2
4 5
2
3 5
2
3 4

出力例2: 2

入力例3: 8
1
2
1
1
1
4
1
3
1
6
1
5
1
8
1
7

出力例3: 4

問題一覧へ戻る