正確なフィッティング C編（paizaランク C 相当）

問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！

問題

下記の問題をプログラミングしてみよう！

データ群にもっともらしい関数を当てはめることをフィッティングと呼び、そのフィッティングした関数を使ってデータ群の特徴、傾向などを調べることを回帰分析と言います。データ分析における基本的な分析手法です。

フィッティングの手法のひとつに最小二乗法があります。これは、それぞれのデータとの誤差の二乗和を最小にする関数を求めるという方法です。
x,y の二次元データにおいて最小二乗法を厳密に言い換えると、当てはめる関数を y = f ( x ) としたとき、Σ ( y_i - f ( x_i ) )² の値が最小となるような関数 f ( x ) を求めるという方法です。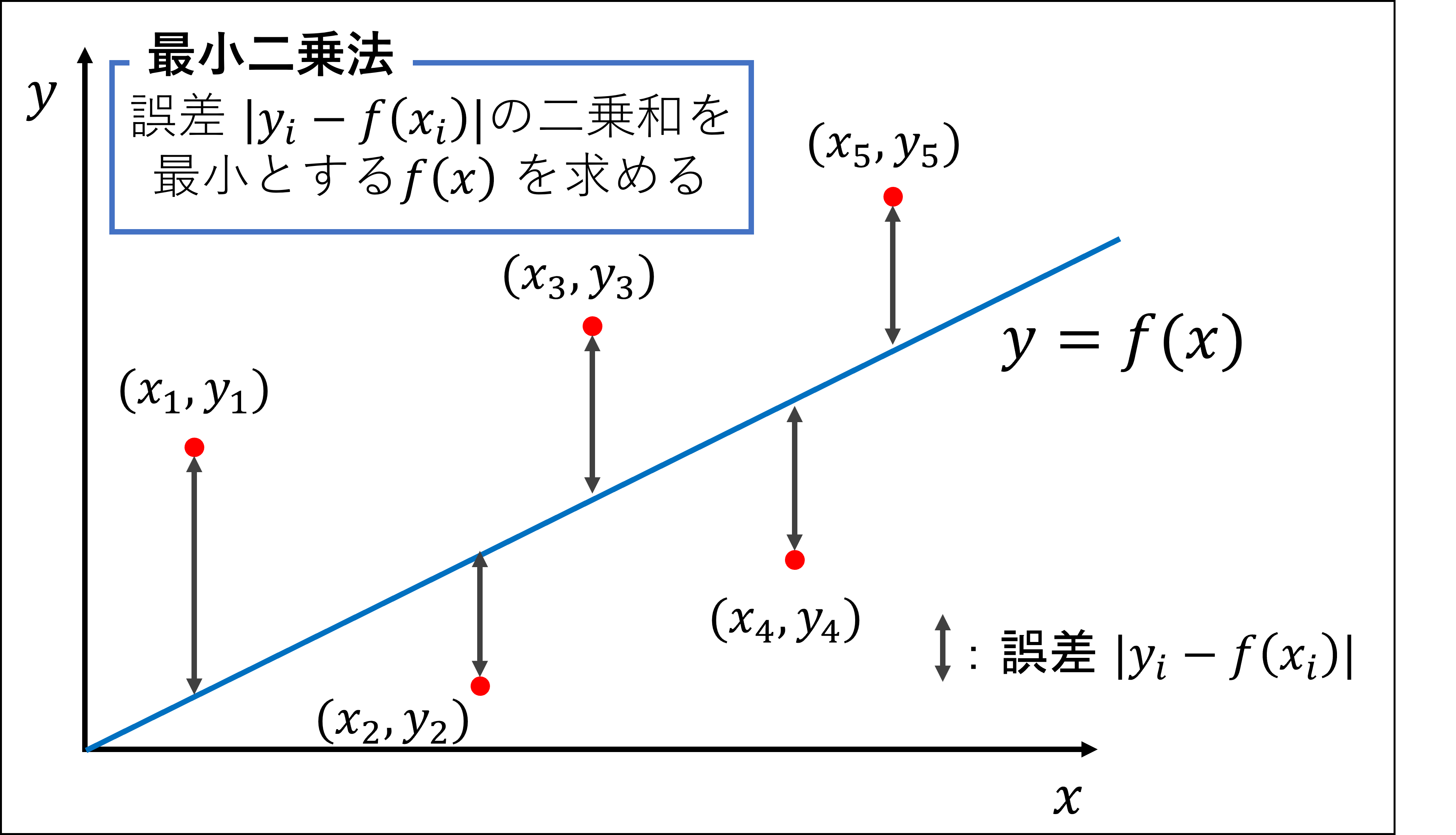

n 個の二次元データが与えられます。タロー君は最小二乗法を用いてこれらのデータを y = αx の形にフィッティングし傾きを求め、その傾きの小数第 5 位を四捨五入した小数 a を求めました。しかし、タロー君はこの傾きを正しく求められたかどうか不安です。タロー君が求めた小数 a が正しいならば Yes、そうでないならば No と出力してください。なお、最小二乗法を利用して厳密に求めた傾き α' の小数第 5 位を四捨五入した値と、タロー君が求めた小数 a が一致したならば、タロー君の小数 a は正しいものとします。

ヒント

x,y の二次元データを y = αx の形にフィッティングするとき、それぞれのデータとの誤差の二乗和を最小とする傾き α' は

Σ x_i y_i / Σ x_i²

となります。

入力される値

a
n
x_1 y_1
...
x_n y_n

・1 行目に、タロー君が求めた小数 a が与えられます。

・2 行目に、与えられるデータの数を表す整数 n が与えられます。

・i + 2 行目に、データ i の x 座標を表す整数 x_i と、データ i の y 座標を表す整数 y_i が与えられます。(1 ≦ i ≦ n)

入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。標準入力からの値取得方法はこちらをご確認ください

期待する出力: タロー君が求めた小数 a が正しいならば Yes、そうでないならば No と 1 行で出力してください。

末尾に改行を入れ、余計な文字、空行を含んではいけません。

条件: すべてのテストケースにおいて、以下の条件を満たします。

・0 ≦ a ≦ 1

・a は小数で、小数第 4 位まで与えられる

・2 ≦ n ≦ 10,000

・n は整数

・0 ≦ y_i ≦ x_i ≦ 10,000 (1 ≦ i ≦ n)

・x_i, y_i は整数 (1 ≦ i ≦ n)

・同じ (x,y) の組は入力されない

入力例1: 0.6556
8
1 0
1 1
2 2
3 1
3 3
4 3
5 2
5 4

出力例1: Yes

入力例2: 0.0001
2
10000 0
10000 1

出力例2: Yes

入力例3: 0.7500
10
1 1
3 3
5 5
7 7
9 9
2 1
4 2
6 3
8 4
10 5

出力例3: No

問題一覧へ戻る