最小全域木 Rust(Beta)編（paizaランク A 相当）

巡回セールスマン問題とは、都市の集合と各都市間の距離が与えられ、全都市をちょうど1回ずつ訪れたのち出発した都市に戻ってくるような経路 (巡回路) のうち最も短いものを求める問題です。

前問までは、順列全列挙による解法と動的計画法による解法を学習しました。これらは巡回セールスマン問題を厳密に解く、厳密解法と呼ばれるアルゴリズムです。これらのアルゴリズムは、都市の数が多くなると計算に時間がかかりすぎるという欠点があります。

ここからは、近似解法について学んでいきます。近似解法とは、厳密に一番良い解 (最適解) ではないものの、ある程度良い解 (近似解) を現実的な時間で求める解法です。ここでは、巡回セールスマン問題に対する 2-近似アルゴリズムを学習しましょう。このアルゴリズムは、最悪でも最適値の 2 倍以下の値を持つ解を出力します。

巡回セールスマン問題に対する 2-近似アルゴリズムの概要は、以下の通りです。

・ 都市をグラフの頂点とみなし、最小全域木 MST を求める
・ MST の辺を複製して二重にしたグラフを作り、一筆書きをする
・ 一筆書きにおいて訪れる都市を先頭から順に並べる。ただし既に訪れた都市には再度訪れないようにして、全都市をちょうど 1 度ずつ訪れる経路 (巡回路) を作る

図を見ながらアルゴリズムの流れを追っていきましょう。



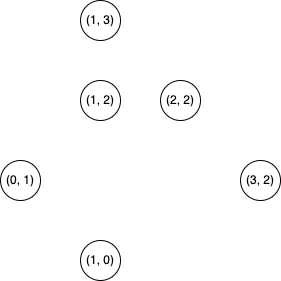
最小全域木を求めます。



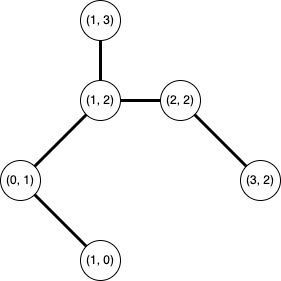
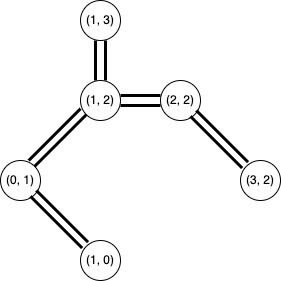
辺を複製して二重にしたグラフを作ります。



都市 (1,3) を始点として一筆書きをします。



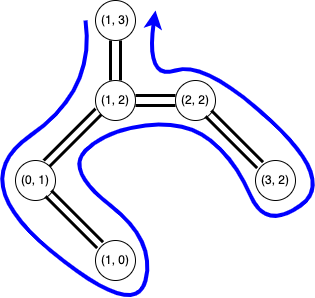
この一筆書きをなぞりながら経路を作ります。ただし、同じ都市を 2 度通らないように注意します。





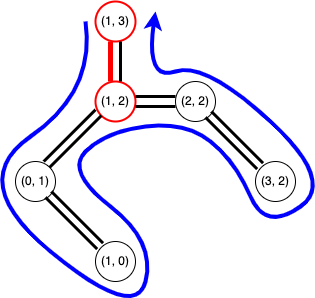
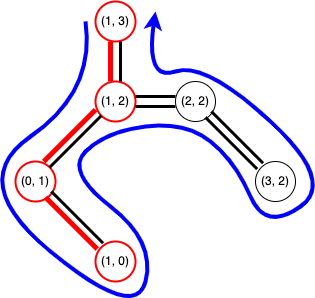
一筆書きをなぞって、都市 (1, 0) まで到達しました。一筆書きを引き続きなぞると次は都市 (0, 1) となりますが、この都市は既に通っているのでスキップします。さらに引き続きなぞると次の都市は (1, 2) となりますが、この都市も既に通っているためスキップします。さらに引き続きなぞると次は都市 (2, 2) で、この都市はまだ通っていないのでスキップしません。



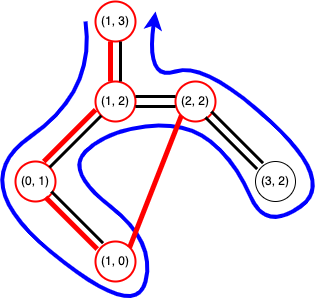
操作を続けると、このような巡回路が得られます。これが2-近似アルゴリズムの出力となります。



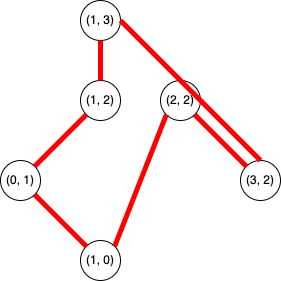
2-近似アルゴリズムを実装するために、ここではまず最小全域木を求める練習をしましょう。

最小全域木を求めるアルゴリズムはいくつかありますが、最も有名なのはおそらくクラスカル法でしょう。クラスカル法とは、以下のようなアルゴリズムです。

・ 都市を頂点とし、辺を 1 本も含まないグラフ G を用意する
・ 都市のペアを結ぶ辺を全て列挙し、E とする
・ E が空になるまで、以下を繰り返す
    ・ E に含まれる辺のうち最も長さが短いものを E から削除して e とする
    ・ e が結ぶ 2 つの都市が異なる連結成分に含まれているなら、G に e を追加する
・ G を最小全域木として出力する

n 個の都市 (都市 0、都市 1、...、都市 n-1) のデータが与えられます。この都市群の最小全域木を求めてください。なお、各都市は二次元平面上の点として与えられ、都市間の距離にはユークリッド距離を用いるものとします。

出力は、最小全域木を構成する辺を各行に 1 つずつ出力してください。各辺は、端点の番号を半角スペース区切りで出力してください。辺や端点の順序は自由です。

なお、答えは一つとは限りません。出力が正しい最小全域木であれば正解と判定されます。