二分探索木への値の追加 Ruby編(paizaランク B 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
このチャプターでは、グラフ理論における二分探索木を扱います。
二分探索木とは、根付き木の一種で、高々各頂点が持つ子の数が高々 2 であり、かつ、次の条件を満たすもののことです。
```
ある頂点の値 V と、その左右の子の値 V_L , V_R について「V_L < V < V_R」が全ての頂点について成り立つ。
```
例として、以下のような根付き木は二分探索木となります。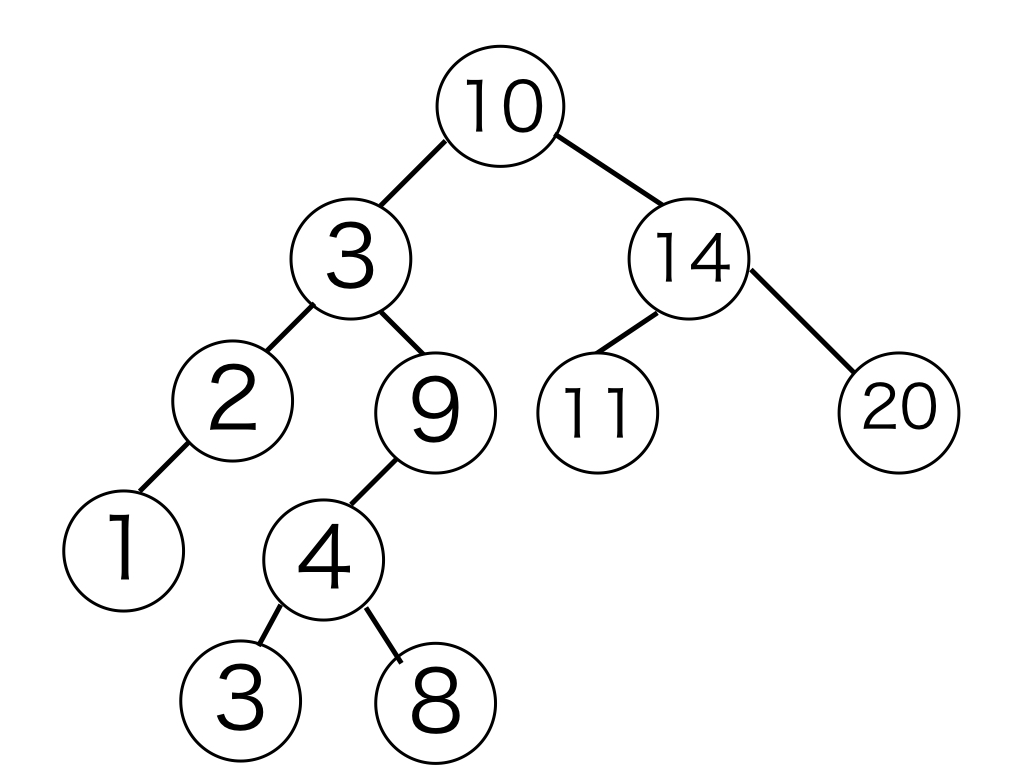
二分探索木 T についての情報と、 T のどの値とも異なる値 V が与えられるので、木全体が二部探索木となるように V を適切な位置に追加した時の V の親子についての情報を出力してください。
例として、上の二分探索木に 13 を追加すると、11 の右の子となります。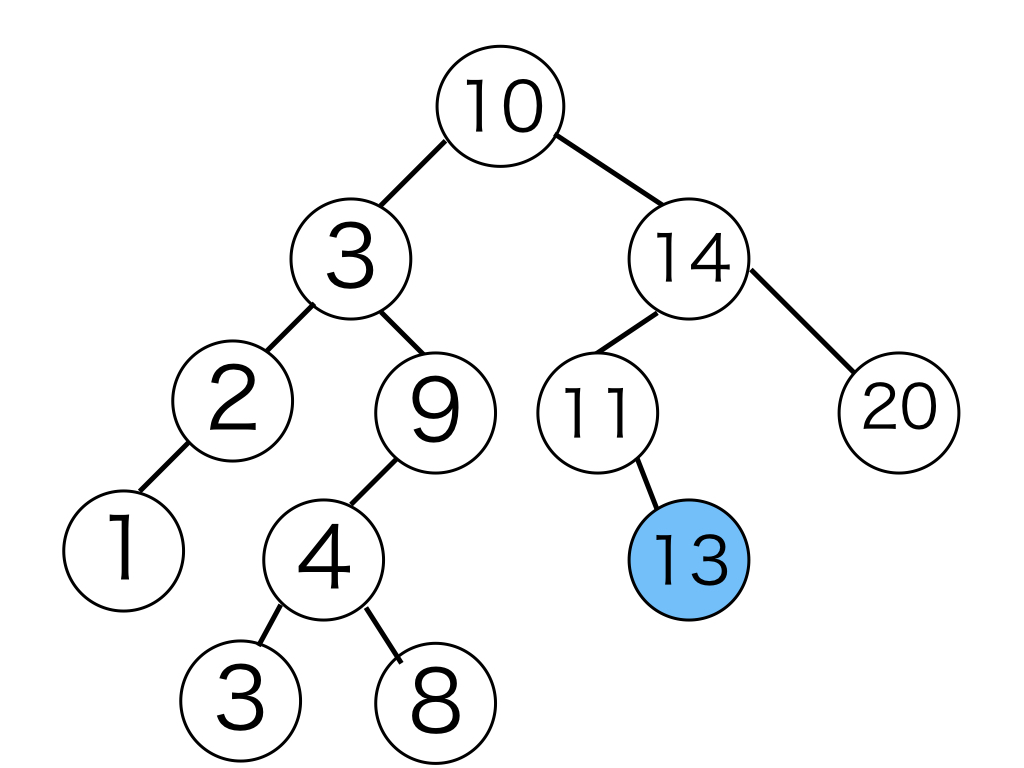
- 入力される値
-
N R
a_1 b_1 LR_1
...
a_{N-1} b_{N-1} LR_{N-1}
V
・1 行目には、二分探索木の頂点の数 N, 二分探索木の根の頂点の値 R が与えられます。
・続く N-1 行のうち、i 行目では、辺の親の値 a_i と子の値 b_i と、子が左右どちらにあるかを表す LR_i が与えられます。(1 ≦ i ≦ N-1)
・N+1 行目では二分探索木に追加したい値 V が与えられます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
P
lr
・木全体が二部探索木となるように V を適切な位置に追加した時の V の親の値 P と、V が P の左右どちらの子であるかの文字 lr を出力してください。
・V が P の左の子である場合には lr として 'L' を、右の子である場合には 'R' を出力してください。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・1 ≦ N ≦ 100
・1 ≦ R ≦ 100,000
・0 ≦ a_i , b_i ≦ 100,000 (1 ≦ i ≦ N-1)
・LR_i は 'L' または 'R'(1 ≦ i ≦ N-1)
・1 ≦ V ≦ 100,000
・与えられる二分探索木の高さは 20 未満であることが保証されている。
・a_i は「根の頂点の値」または「親の頂点が確定している頂点の値」であることが保証されている。
・与えられる木の中に(V も含め)同じ値が 2 つ以上含まれていないことが保証されている。
- 入力例1
-
3 7
7 1 L
7 10 R
4
- 出力例1
-
1
R
- 入力例2
-
10 88184
88184 23687 L
23687 62695 R
62695 42223 L
42223 43627 R
43627 52030 R
62695 69436 R
43627 43506 L
42223 28016 L
69436 79231 R
70258
- 出力例2
-
79231
L

