セルとセルを繋ごう Rust(Beta)編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
(電脳言語のオルダーソンループで出題された問題のヒント問題です。8 言語での解答コードと解説が用意されています。)
縦に H マス、横に W マスの長さの二次元グリッドが与えられます。それぞれのセルには、0 以下 の値をとる整数が与えられます。
このグリッドから連結したセルの集合を選んだ時、その集合のスコアを、セルに書かれた整数の和と定義します。 ただし、セルの集合が連結であるとは、セル集合内のある一つのセルから、上下左右に繋がっている集合内のセルを辿ることで、集合内の全てのセルを辿れることを指します。 例えば、下の図では、黒いセルの集合は、左の 2 つの例では連結であり、右の 2 つの例では連結ではありません。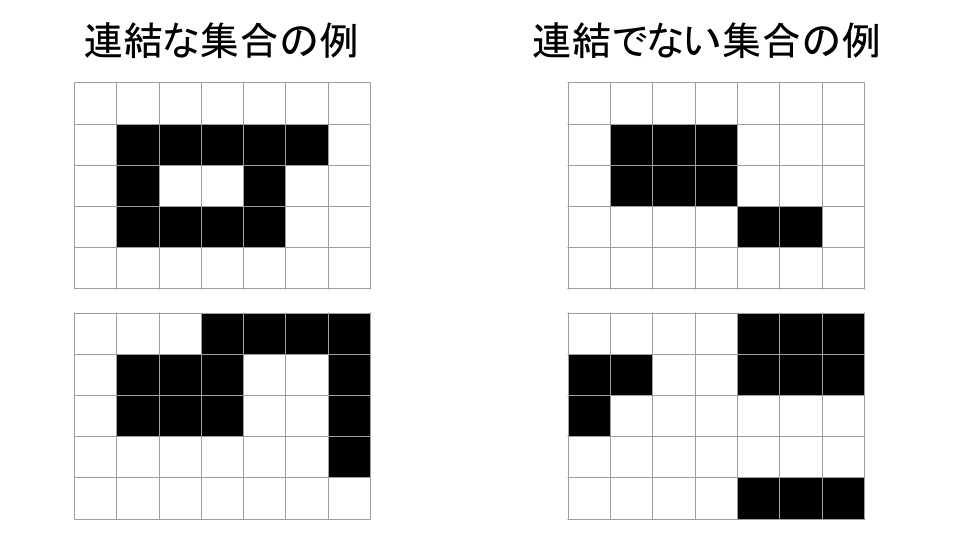
上から i 番目、左から j 番目のセルをセル (i, j) とします。セル (si, sj) と セル (gi, gj) が連結となるようなセルの集合のうち、スコアが最大となるようなもののスコアを出力してください。
入力例 1 では、以下のような集合が最適で、スコアの最大値は -43 となります。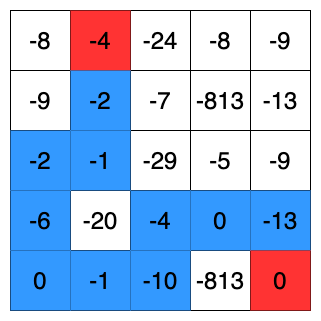
- 入力される値
-
H W
si sj gi gj
g_{1, 1} g_{1, 2} ... g_{1, W}
g_{2, 1} g_{2, 2} ... g_{2, W}
...
g_{H, 1} g_{H, 2} ... g_{H, W}
・ 1 行目に二次元グリッドの縦と横の長さを表す整数 H, W が半角スペース区切りで与えられます。
・ 2 行目に、連結にしたい 2 つのセルの位置を表す si, sj, gi, gj が半角スペース区切りで与えられます。
・ 続く H 行のうちの i 行目 (1 ≦ i ≦ H) には、W 個の整数が半角スペース区切りで与えられます。
・ i 行目の j 番目 (1 ≦ j ≦ W) の整数 g_{i, j} はグリッドの i 行 j 列目のセルに書かれている整数を表します。
・ 入力は合計で H + 2 行となり、入力値最終行の末尾に改行が 1 つ入ります。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
・ セル (si, sj) と セル (gi, gj) が連結となるようなセルの集合のうち、スコアが最大となるようなもののスコアを出力してください。
・ 末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
全てのテストケースにおいて, 以下の条件を満たします。
・ 5 ≦ H ≦ 30
・ 5 ≦ W ≦ 30
・ 1 ≦ si, gi ≦ H
・ 1 ≦ sj, gj ≦ W
・ -1,000 ≦ g_{i, j} ≦0(1 ≦ i ≦ H, 1 ≦ j ≦ W)
- 入力例1
-
5 5
1 2 5 5
-8 -4 -24 -8 -9
-9 -2 -7 -813 -13
-2 -1 -29 -5 -9
-6 -20 -4 0 -13
0 -1 -10 -813 0
- 出力例1
-
-43

