進化戦略のプロシージャ F#(Beta)編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
(電脳言語のオルダーソンループで出題された問題です。8 言語での解答コードと解説が用意されています。)
この問題は前問 (ダンジョンのデッドロック 5) と同じ内容ですが、制約だけが大きくなっています。
あなたは RPG のダンジョンの設計をしています。
そのダンジョンには N 個の部屋が用意されており、それぞれの部屋は 1, 2, ..., N で表されます。このダンジョンでは 1 部屋に 1 プレイヤーしか滞在できません。
また、プレイヤーは M 人いて、現在 i (1 ≦ i ≦ M) 番目のプレイヤーは部屋 S_i (1 ≦ S_i ≦ N) に滞在しています。
ダンジョンをクリアするには M 人のプレイヤーはそれぞれ、部屋 T_i (1 ≦ T_i ≦ N) に移る必要があります。
しかし、部屋の移動は各プレイヤーが好きなタイミングでおこなうため、部屋を移動しようと思ってもその部屋はまだ別のプレイヤーが滞在しているかもしれません。
その場合はプレイヤーは部屋を移動することができません。移動先にいるプレイヤーが先に移動するのを待つ必要があります。
なお、同じタイミングで同時に移動をおこなうことはできません。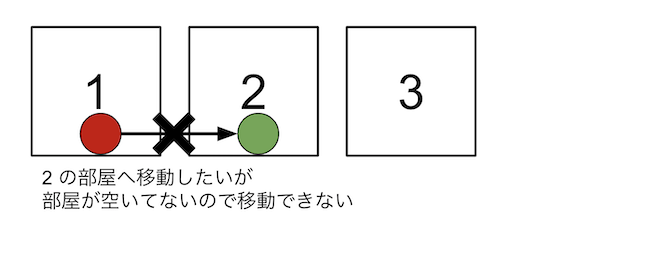
ここで、問題が生じました。もしかすると、ダンジョンの移動をどのような順番でしても、移動先の部屋にプレイヤーが居て移動することができないプレイヤーが現れる可能性があります。
例えば下の図では、 3 番目の部屋に滞在していたプレイヤーは移動ができていますが、 1 番目の部屋に滞在していたプレイヤーと 2 番目に滞在していたプレイヤーはお互いに部屋を移動することができません。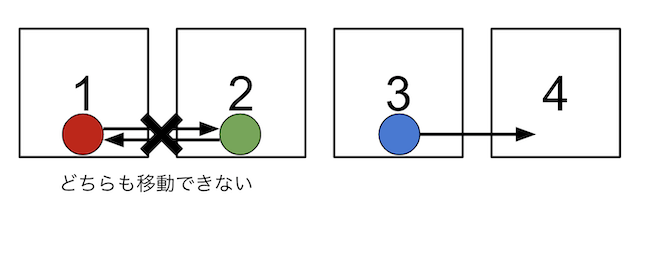
このように、どのような順番で部屋を移動しても、部屋を移動することができないプレイヤーがいる状態のことをデッドロックと呼ぶことにします。
あなたの仕事はデッドロックが起きるか起きないかを判定することです。
ただし、滞在している部屋と移動先の部屋が同じ場合、つまり S_i = T_i (1 ≦ i ≦ M) の場合、そのプレイヤーは移動ができることとします。
- 入力される値
-
N M
S_1 T_1
S_2 T_2
...
S_M T_M
・1 行目には、ダンジョンの部屋の数 N ,プレイヤー数 M がこの順で半角スペース区切りで与えられます。
・続く M 行のうちの i 行目 (1 ≦ i ≦ M) には、i 人目のプレイヤーの現在滞在している部屋 S_i, 移動した後に滞在する部屋 T_i がこの順で半角スペース区切りで与えられます。
・入力は合計で M + 1 行となり、 入力値最終行の末尾に改行が 1 つ入ります。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
・デッドロックが発生する場合は "Yes" を、発生しない場合は "No" を出力してください。末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて、以下の条件を満たします。
・1 ≦ N ≦ 100,000
・1 ≦ M ≦ N
・1 ≦ S_i ≦ N (1 ≦ i ≦ M)
・1 ≦ T_i ≦ N (1 ≦ i ≦ M)
・S_i ≠ S_j (1 ≦ i, j ≦ M, i ≠ j)
・T_i ≠ T_j (1 ≦ i, j ≦ M, i ≠ j)
- 入力例1
-
4 3
1 2
2 1
3 4
- 出力例1
-
Yes
- 入力例2
-
6 4
5 6
1 2
2 4
3 5
- 出力例2
-
No
- 入力例3
-
3 3
1 1
2 2
3 3
- 出力例3
-
No

