選択ソート (paizaランク B 相当)

順序付け可能なデータの列を、昇順または降順に並び替える操作をソートと呼びます。「データ」は、数値や文字列、オブジェクトなどあらゆるものを指します。


ソート処理はいたるところで利用されています。


・得点表を元にしてランキングを作成する

　　　　一番素朴なソートの使い方です。


・データの集まりから、上位k個を取ってくる

　　　　ソートをしてから先頭のk個を取ればよいです。


・貪欲アルゴリズムの前処理

　　　　データを大きい (小さい) 順に貪欲に処理を行っていくようなアルゴリズムの前処理として、ソートは有効です。


---


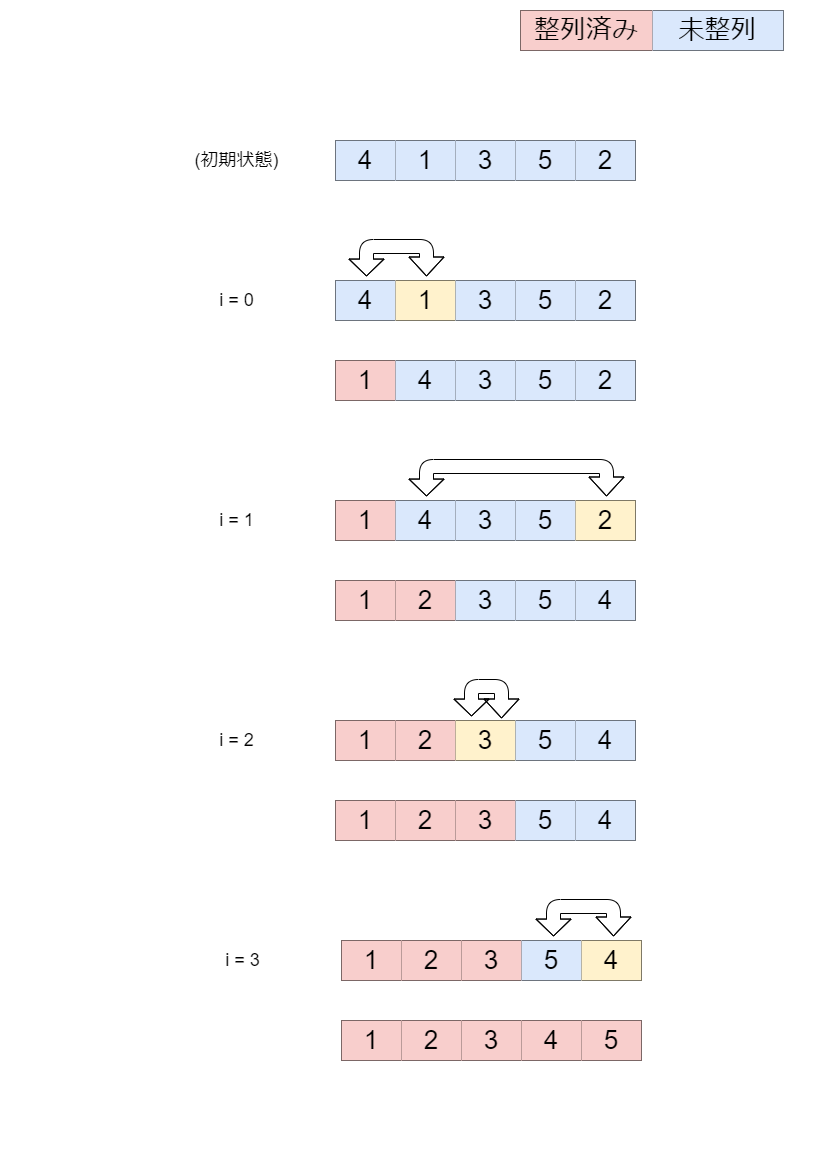
選択ソート (昇順) は、データ列を「整列済み」と「未整列」の2つに分け、「未整列な配列」の最小値を取り出し、「整列済み配列」の末尾に付け加えることを繰り返す手法です。「未整列な配列」の要素数が 1 になるまで処理を繰り返すと、1つの「整列済み配列」が得られます。


選択ソート (昇順) は以下のようなアルゴリズムです。初期状態では配列全体 A[0] ~ A[n-1] を「未整列」とします。

selection_sort(A : 配列, n : Aの要素数)
    for i = 0 to n-2
        // A[i] ~ A[n-1] の最小値を見つけ、A[i]と交換する
        // つまり、整列済みとなっている A[0] ~ A[i-1] の末尾に、A[i] ~ A[n-1] の最小値を付け加える
        
        // A[i] ~ A[n-1] の最小値の位置を保存する変数 min_index を用意
        // 暫定的に A[i] を最小値とする
        min_index <- i

        // 最小値を探す
        for j = i+1 to n-1
            if A[j] < A[min_index] then
                min_index = j

        // A[i] と A[min_index]を交換
        swap(A[i], A[min_index])

        // A[0] ~ A[i] が整列済みになった

選択ソートの計算量を考えます。最も多くの計算ステップがかかるのは、二重 for ループ中にて値を比較する処理です。よって、この処理が何回行われるかに注目し、計算量を導きます。この処理は、各 i について n-i-1 回行われます。つまり、この処理は全体で n-1 + ... + 1 = (n-1)*n/2 = (n^2-n)/2 回行われます。よって、選択ソートは O(n^2) のアルゴリズムとなります。


選択ソートは、入力によって効率が左右されないアルゴリズムです。


---


では、要素数 n の数列を昇順にソートする選択ソートのプログラムを作成してください。上の疑似コードに従って実装してください。アルゴリズムが正しく実装されていることを確認するために、各 i についてその処理が終わった時点での配列を出力してください。