シェルソート Bash(Beta)編（paizaランク B 相当）

シェルソートは、挿入ソートを改良したアルゴリズムです。挿入ソートが整列済みのデータ列に強いことを利用しています。

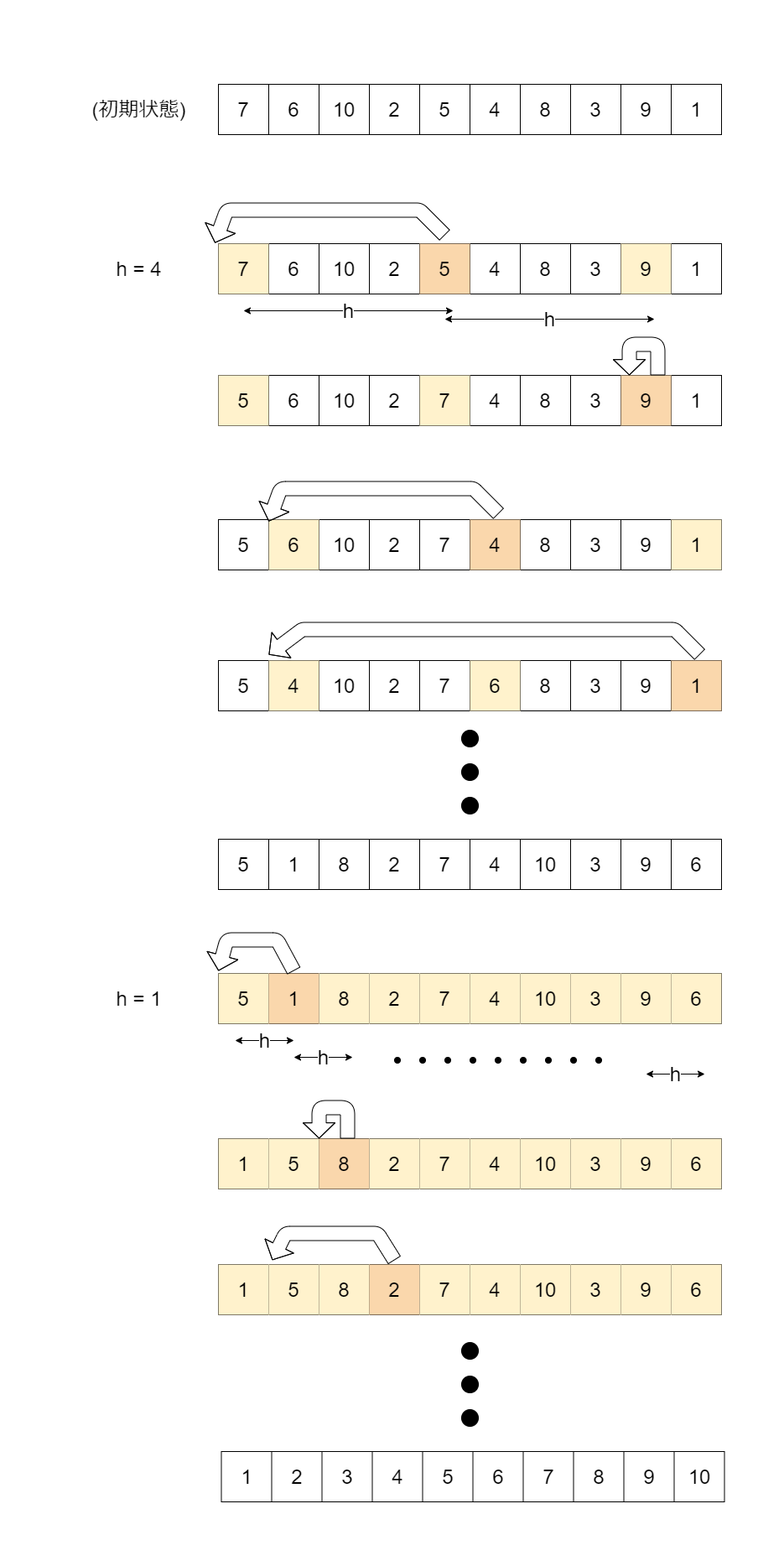
シェルソートでは、データ列において一定の間隔 h だけ離れた要素たちからなる部分列を対象とした挿入ソートを、h を小さくしながら (間隔を狭めながら) 繰り返してソートを行っていきます。h は適当に大きな値から始め、段階的に小さくしていき、最終的に 1 にします。h が 1 のとき、間隔が 1 離れた要素たちからなる部分列というのは元のデータ列そのものですから、このとき単純な挿入ソートを行うことになります。この時点でデータ列は既にほとんど整列済みとなっていることが期待されるため、ここで挿入ソートの強みが活かされます。

シェルソート (昇順) は以下のようなアルゴリズムです。

insertion_sort(A : 配列, n : Aの要素数, h : 間隔)
    // アルゴリズムが正しく実装されていることを確認するために導入するカウンタ変数、ソート処理には関係がないことに注意
    num_of_move <- 0

    for i = h to n-1
        // A[i] を、整列済みの A[i-ah], ..., A[i-2h], A[i-h] の適切な位置に挿入する

        // 実装の都合上、A[i] の値が上書きされてしまうことがあるので、予め A[i] の値をコピーしておく 
        x <- A[i]

        // A[i] の適切な挿入位置を表す変数 j を用意
        j <- i-h

        // A[i] の適切な挿入位置が見つかるまで、A[i] より大きい要素を後ろにずらしていく
        while j >= 0 AND A[j] > x
            A[j+h] = A[j]
            j -= h
            num_of_move++
        
        // A[i] を挿入
        A[j+h] <- x

shell_sort(A : 配列, n : Aの要素数, H : 間隔列)
    for h in H
        insertion_sort(A, n, h)

シェルソートの計算量は間隔列 H に強く依存します。シェルソートの計算量解析を正確に行うことは難しく、未解決です。いくつかの有名な間隔列に対しては計算量解析が行われており、例えば h_i = 3h_{i+1} + 1を満たす整数列 (..., 364, 121, 40, 13, 4, 1) を間隔列として採用した際のシェルソートは、平均計算量が O(n^{1.25}) になることが知られています。

---

では、要素数 n の数列を昇順にソートするシェルソートのプログラムを、上の疑似コードに従って実装してください。数列 h_1, ... , h_k が入力として与えられるので、それを間隔列として採用してください。なお、この数列は上で示した漸化式h_i = 3h_{i+1} + 1を満たしています。

アルゴリズムが正しく実装されていることを確認するために、各間隔 h_i について、num_of_move を出力してください。