クイックソート Ruby編（paizaランク B 相当）

クイックソートは、ピボットと呼ばれる値を1つ選び、それを基準としてデータ列を「ピボット未満の要素からなるデータ列」と「ピボット以上の要素からなるデータ列」に二分することを再帰的に行うアルゴリズムです。このアルゴリズムは、問題を小さな問題に分割して解くことを繰り返すことによって元の問題の答えを得る手法である「分割統治法」に基づいており、実用的なソートアルゴリズムの中で最も高速であるとされています (名前に quick と付いていることからも、その高速さが評価されていることが窺えます)。

ピボットの選び方にはいくつか種類があり、

・データ列の先頭をとる
・データ列の末尾をとる
・データ列からランダムにとる
・データ列からランダムに2つとり、その中央値をとる

等が例として挙げられます。今回は、2つ目の方法でピボットを選択することにします。

ピボットを選択したら、データ列の先頭からデータを1つずつ確認していき、ピボット未満のデータをデータ列の先頭に集めます。そして、ピボットより左側がピボット未満、右側がピボット以上となるようにピボットを移動し、そこでデータ列を二分します。そして、分割された2つのデータ列に対して再び同じ操作を繰り返します。

クイックソート (昇順) は以下のようなアルゴリズムです。

// アルゴリズムが正しく実装されていることを確認するために導入するカウンタ変数、ソート処理には関係がないことに注意
count <- 0

/**
    A[left] ~ A[right-1] をクイックソートする
    配列 A をクイックソートするには quick_sort(A, 0, n) を呼び出す
*/
quick_sort(A : 配列, left : 整数, right : 整数)
    // ソートする範囲の長さが1以下の場合は何もしない
    if left+1 >= right then
        return

    // データ列の末尾 A[right-1] をピボットとする
    pivot <- A[right-1]

    // ピボット未満のデータを挿入する位置を保持する変数を用意
    cur_index <- left

    for i = left to right-2
        if A[i] < pivot then
            swap(A[cur_index], A[i])
            cur_index++

            count++

    // ピボットを A[cur_index] へ移動し、データ列を分割する
    swap(A[cur_index], A[right-1])
    
    // 分割されたデータ列に対して再帰的にクイックソートを行う
    quick_sort(A, left, cur_index)
    quick_sort(A, cur_index+1, right)

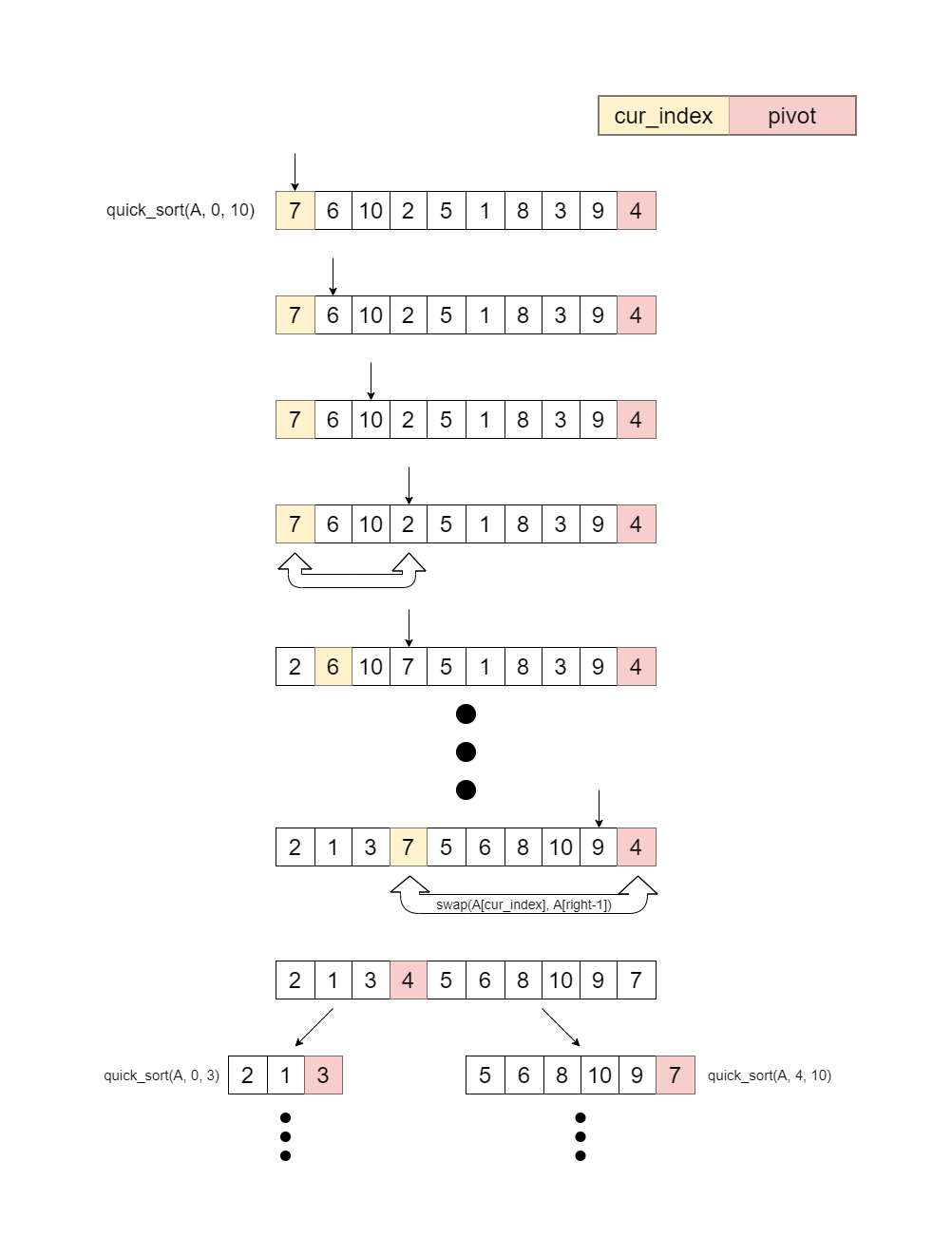
クイックソートは、データ列がバランスよくちょうど半分ずつに分割されていけば、データ列のサイズ n に対して約 log n 段にわたり分割が行われることになり、最も効率よくソートを行うことができます。データ列がバランスよく分割されるかどうかは、「ピボットの選び方とデータ列の相性」に強く依存しています。クイックソートの平均計算量は O(n log n) であり、最悪計算量は O(n^2) であることが知られています。

---

では、要素数 n の数列を昇順にソートするクイックソートのプログラムを、上の疑似コードに従って実装してください。アルゴリズムが正しく実装されていることを確認するために、数列をソートした結果に加え、クイックソート後の count の値を出力してください。