ハノイの塔（paizaランク A 相当）
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！
シェア用URL:
ツイートする
問題
下記の問題をプログラミングしてみよう！
ハノイの塔というパズルがあります。
3つの杭があり、左から順にA,B,Cの杭とします。
杭Aに円盤が下から大きい順に n 個重なって置かれています。
この円盤は必ず1つ上の円盤は下の円盤より小さくなくてはいけないルールがあります。
このルールを守りながらAの杭からCの杭へ円盤を動かす操作をするパズルです。
例えば3つの円盤が入力として与えられる場合、その時の最短手順は以下の通りになります。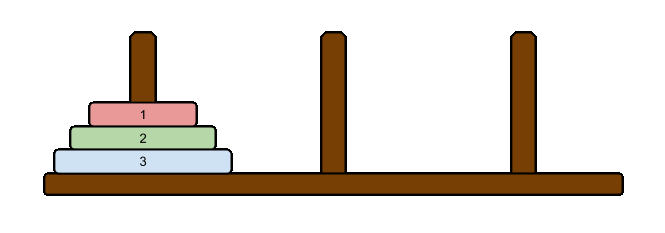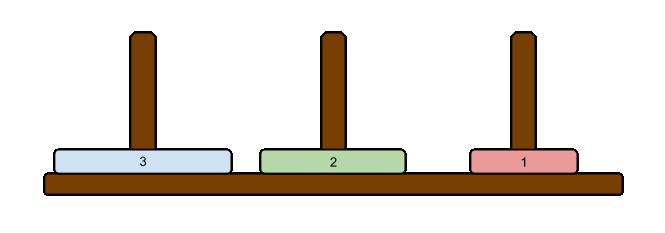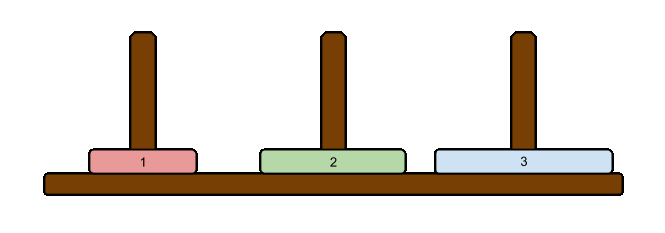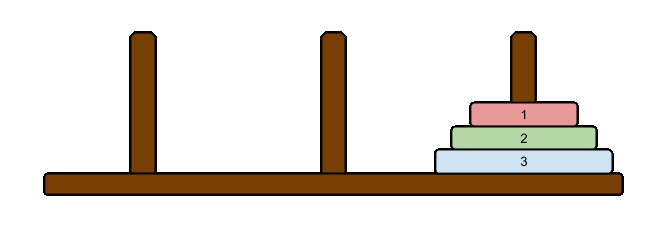
この時、円盤の数に寄らず最短手順は常に一意に決まります。
円盤の数 n が与えられます。1つも動かしていない状態を t = 0 とし、円盤を動かした回数を t とします。
円盤の数 n と、円盤を動かした回数 t が与えられるので n 個の円盤を最短手順で動かしていった時に円盤を動かした回数 t の状態を出力してください。
- 入力される値
-
入力は以下のフォーマットで与えられます。
n t
入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
n 個の円盤を最短手順で動かして行った時、 t 回動かした時点の各杭に積み上がっている円盤を出力してください。
1行目を杭A、2行目を杭B、3行目を杭Cとし、各行の一番左を杭の一番下として円盤の大きさを 1 から n の数字でスペース区切りで出力して下さい。
1つも円盤がない杭の行には「-」と出力して下さい。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
1 ≦ n ≦ 16
1 ≦ t ≦ 2^n - 1
- 入力例1
-
3 4
- 出力例1
-
-
2 1
3
- 入力例2
-
4 6
- 出力例2
-
4 1
3 2
-
