最大流問題 1 Rust(Beta)編（paizaランク B 相当）

このメニューでは、ネットワークフローの最も基本的な問題である最大流問題を解いていきます。

まずは、ネットワークフローとは何かについて理解しましょう。ひとことでいうと、ネットワークフローとは、グラフ上で流れを考える問題です。たとえば、各地点を水道管でつないだグラフを考えてみましょう。このグラフ上で、ある地点から別の地点へ、一定の水を流し続けることを考えます。当然ですが、始点と終点以外では、各地点に入ってくる水の量と出ていく水の量は同じでなければなりません。このとき、流れる水は分岐したり合流したりして、いくつかの経路をたどって終点まで到着します。この水の流れのことを、フローと呼びます。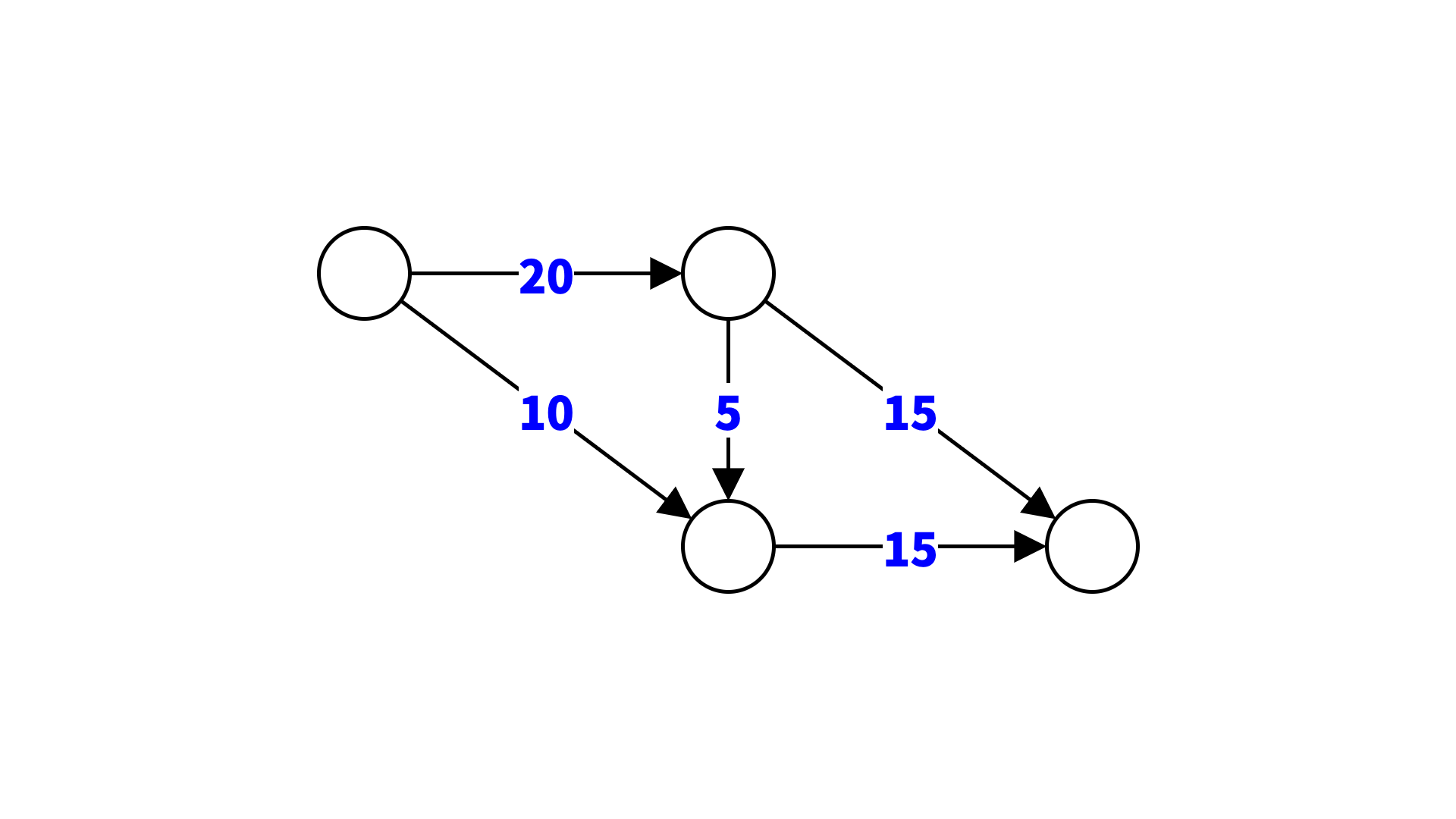



この例では、常に (単位時間あたり) 30 L の水が流れつづけています。この流れる水の量を、フローの流量と呼びます。

現実世界では、各辺に流すことのできる最大の量 (容量) が決まっていることが多いでしょう。 そのような制約が与えられたときに、どれだけ大きい流量のフローを流せるかを考えるのが、最大流問題です。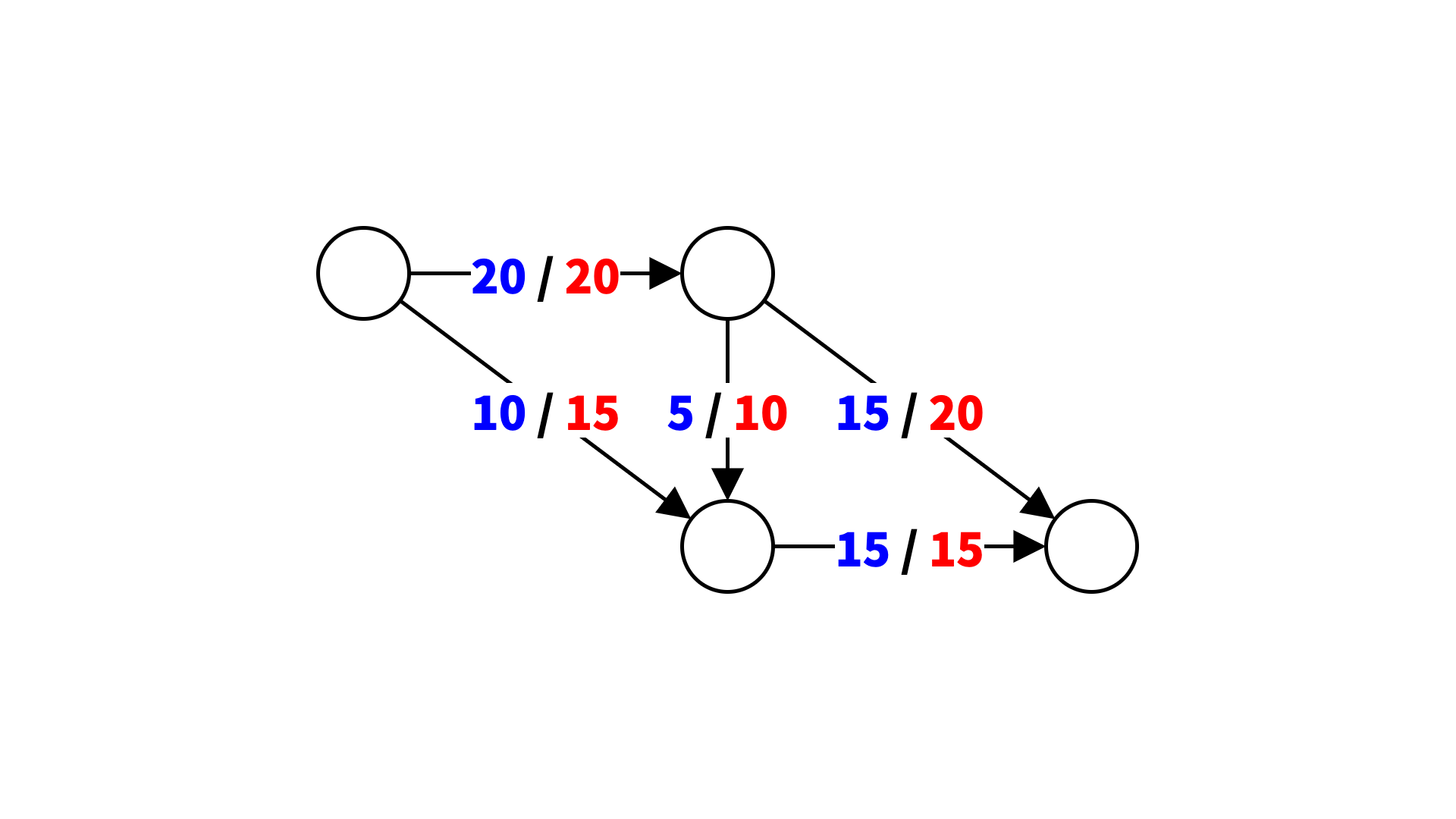



赤い文字で表示されている部分が容量になります。
上の例では、中央の辺を使わずに目一杯流すことで、さらに 5 L 多く流すことができます。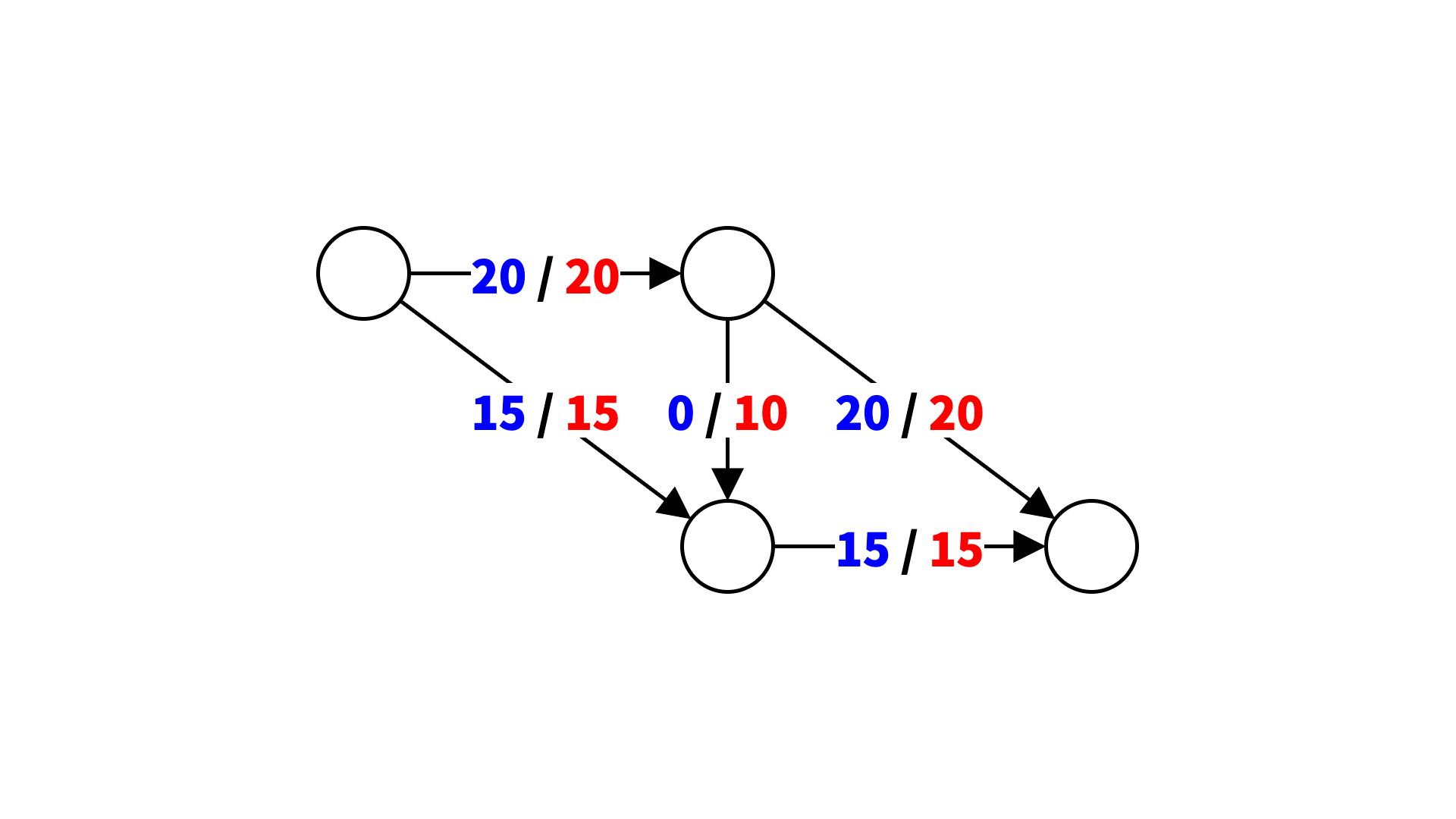



では、手始めに簡単なネットワークフローの問題を解いてみましょう。

辺に容量の制約がある n 頂点 m 辺のグラフが与えられます。各頂点には 1 から n までの番号がついており、各辺は頂点 a_i から頂点 b_i へ向かうもので、容量が c_i になっています。(1 ≦ i ≦ m)
このグラフ上で、始点 s から終点 t へ流量 1 のフローを流せるかどうかを判定してください。

(ヒント)

すべての辺の容量は 1 以上なので、始点 s から終点 t へ流量 1 のフローを流せることと、始点 s から終点 t への経路が存在することは同じになります。