多重辺・有向グラフ (辺入力)（paizaランク B 相当）

いくつかの頂点と、それらのうち 2 つの頂点を結ぶ辺の集合をグラフといいます。特に、辺に向きがつけられている場合は有向グラフといいます。下の図は、頂点の数が 5 の有向グラフの一例です。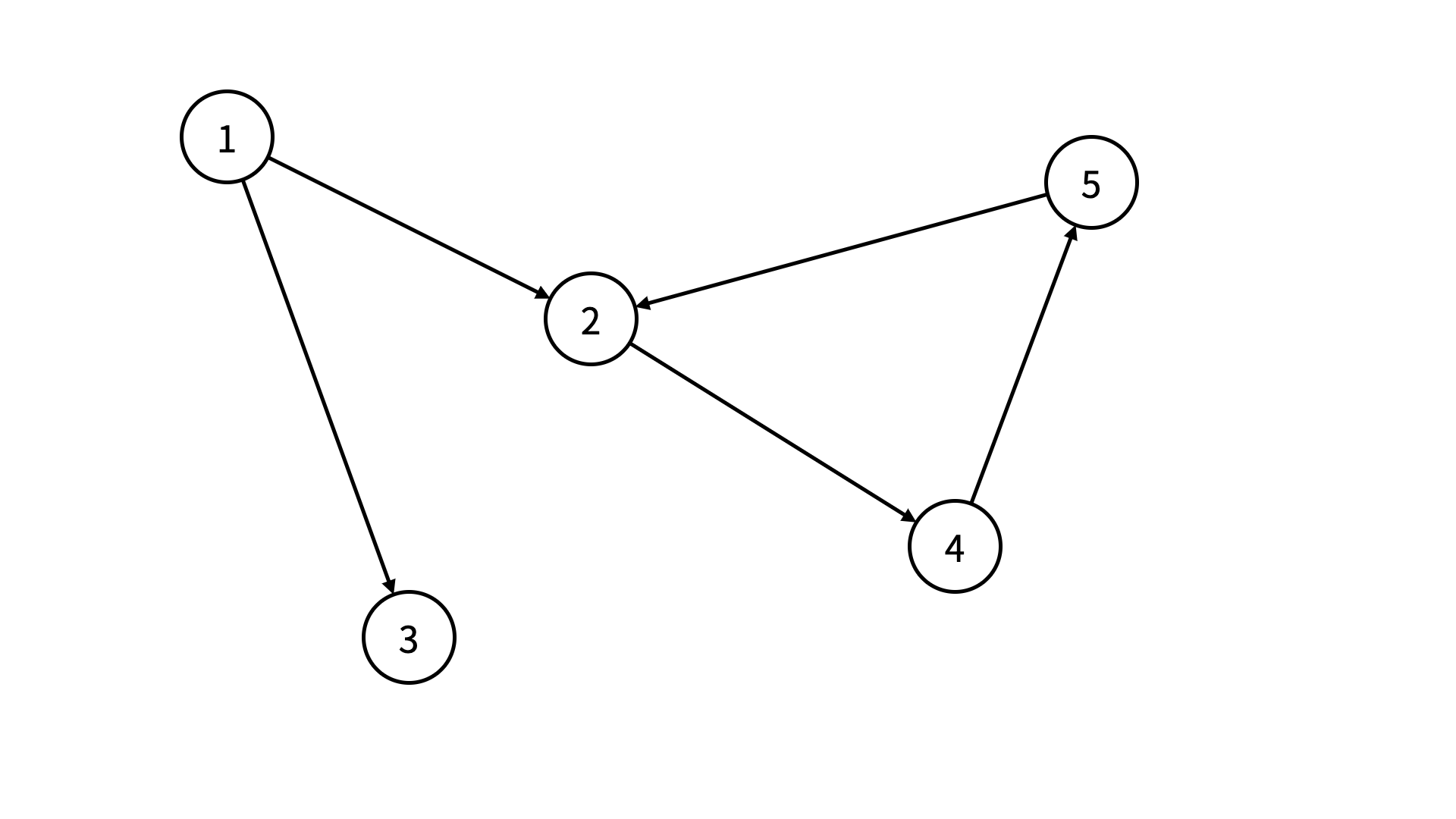



1, ..., n の番号がついた n 個の頂点と、1, ..., m の番号がついた m 個の辺からなる有向グラフを考えます。

整数 n, m と、m 個の頂点の組 (a_1, b_1), ..., (a_m, b_m) が与えられます。

頂点の組 (a_i, b_i) は、頂点 a_i から 頂点 b_i に向かって辺が伸びていることを表します。

そして、これら以外に辺はありません。

このとき、次のような形式で表される「多重辺」の存在する頂点の組をすべて出力してください。


同じ頂点の組 (順番を考慮しない) をつないでいる複数の辺を有向グラフの多重辺といいます。
下の図は、多重辺を含む有向グラフの一例です。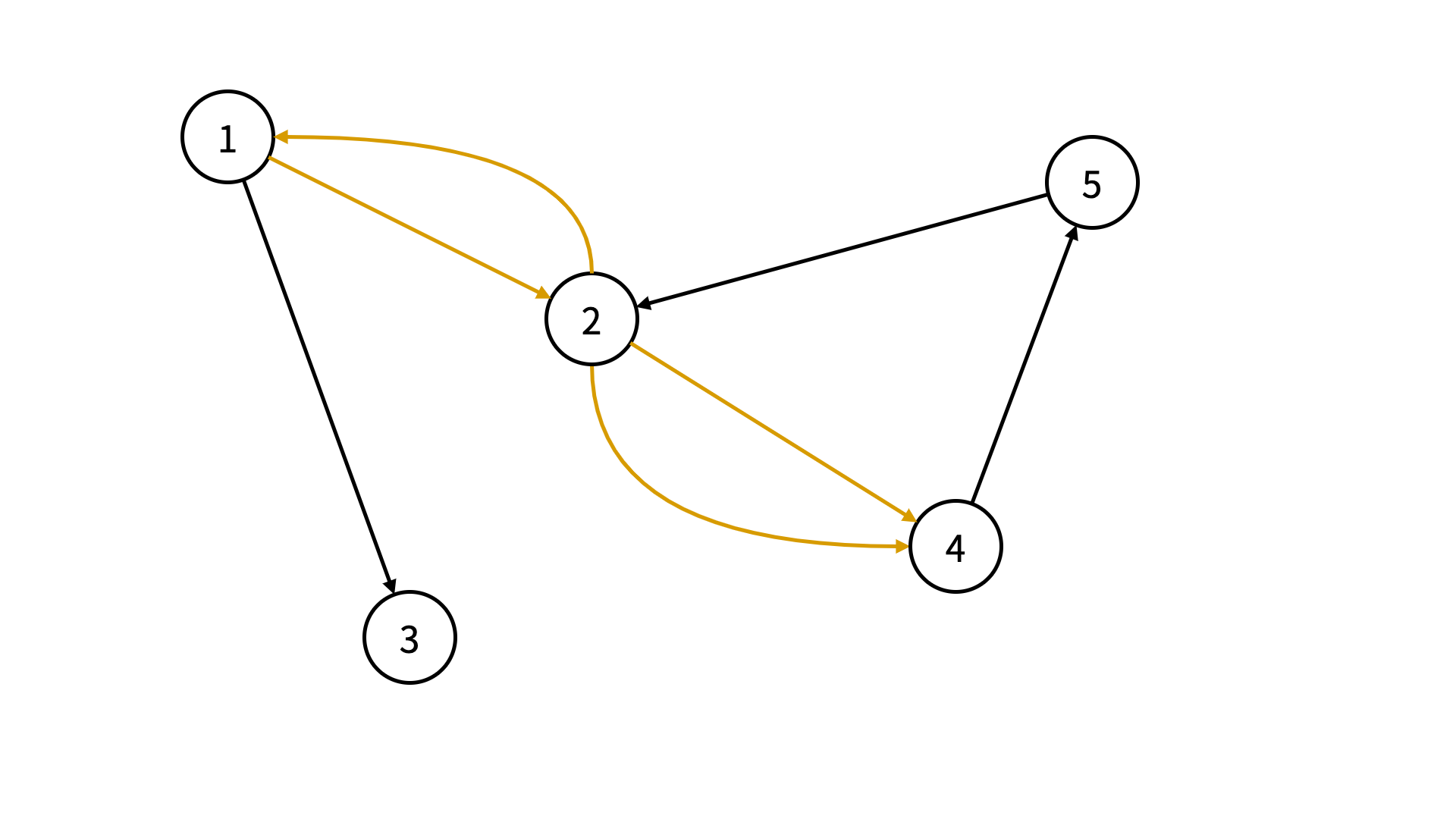





ただし、a_i と b_i は異なる頂点であることが保証されます。