RSA 暗号の作成（文字列） Erlang(Beta)編（paizaランク A 相当）

ここまで学んできた知識を利用して、RSA 暗号で暗号化をしてみましょう。
RSA 暗号で暗号化をするために、その暗号化・解読方法をおさらいしましょう。

＜準備＞
適当な素数 p , q を用意し、 n = pq , n' = (p-1)(q-1) とおく。
e は gcd(e , n') = 1 を満たす適当な整数とし、あらかじめ de ≡ 1 (mod n') を満たす自然数 d を用意する。

＜手順＞
1. 受信者は n と e を公開しておく。
2. 送信者は、数値 M を送信したい時は、代わりに数値 E = M^e mod n を送信する。
3. E^d mod n を求めると元の数値 M が得られる。

送信する数値にルールを決めて、ASCIIコードを利用することで RSA 暗号を用いて英文を送ることができます。
今回の問題では、次のような送信のルールを設定します。

・暗号化前の数字 M は 28 ビットです。
・この数字を上位ビットから 7 ビットずつに区切った時に得られる 4 つの数字が、 4 つの文字の ASCII コードに対応しています。
ただし、数字が 0 の時は、そこに文字がないことを表しているものとします。ただし、 0 は後ろの文字から順に現れる必要があります。
S[0]を 1 文字目、S[3] を 4 文字目とした時の文字と数字の位置の関係は以下の通りです。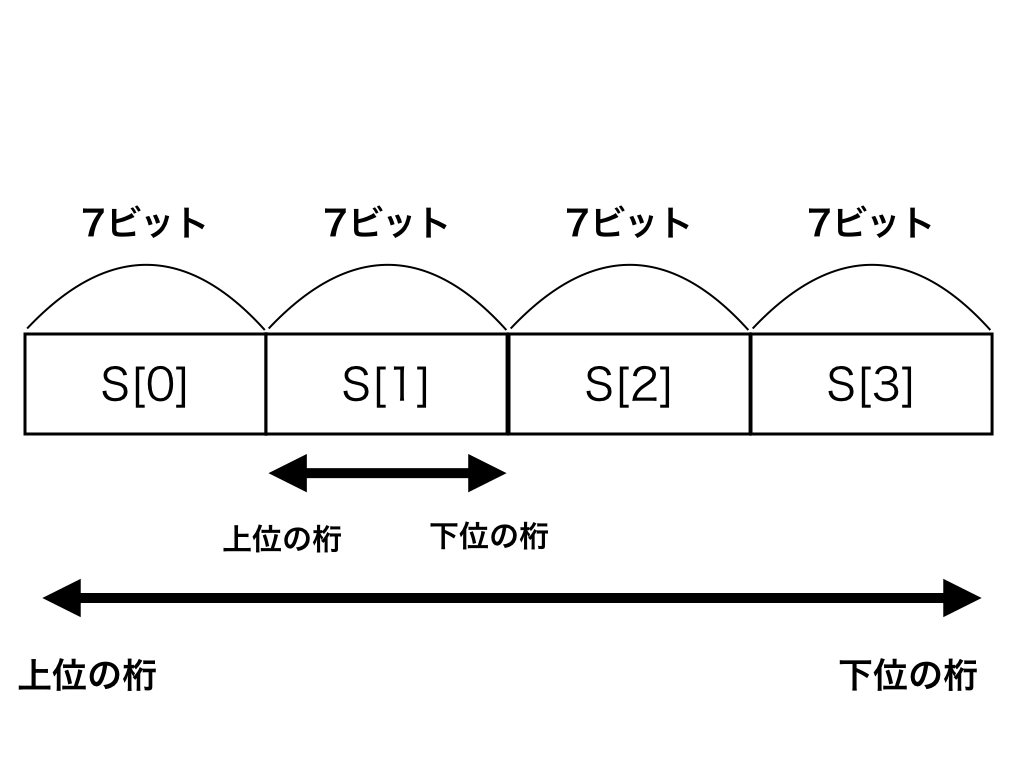



例として、暗号化前の数字が 166908032 の場合を考えます。
これを符号なしの 2 進数にして 7 桁ずつで区切ると、1001111/1001011/0100001/0000000 となるので、
S[0] = 1001111 , S[1] = 1001011 , S[2] = 0100001 , S[3] = 0000000 が得られます。
これを 10 進数に直すと、S[0] = 79 , S[1] = 75 , S[2] = 33 , S[3] = 0
0 である S[3] 以外の数字を ASCII コードを用いて文字に直すと、文字列 「OK!」 が得られます。

この問題では、あなたが暗号を作ってみましょう。
復号に必要な数値 n , e と暗号化した後の数値 E , 暗号化前の文字列 S（最大 4 文字） を出力してください。
n , e , E から S が得られた場合（復号が可能である場合）は正答となり、それ以外の場合は誤答となります。

暗号を作成したら、ぜひ周りの人に共有して解いてみてもらいましょう！