値の計算 JavaScript編(paizaランク B 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
N 種類のそれぞれ決まった抵抗値を持った抵抗のみで構成された回路があります。
i 番目の抵抗は抵抗名 s_i 、抵抗値 w_i です。
回路の始点と終点は1つだけです。
各抵抗は直列または並列につながれています。
回路全体での抵抗値を求めてください。
抵抗値の計算法則は以下のとおりです。
2つの抵抗値A,Bがある場合
・ 直列 A + B
・ 並列 1 / (1 / A + 1 / B)
以下に例を示します。
抵抗がそれぞれ A = 100, B = 150, C = 200 であり、左から A が直列, A と B が並列, C が直列で接続されています。
先の抵抗値の計算法則に従うと式は回路図の下に書かれたようになります。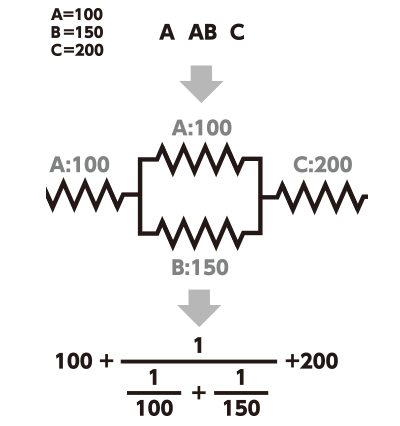
この例の場合、入力は以下のように与えられます。
3
A 100
B 150
C 200
3
A AB C
特に、抵抗のつなぎ方を表す最終行の文字列に注意してください。 A B のように空白区切りの場合は直列、AB のように空白で区切られていない場合は並列でつながれていることを表します。
回路全体の抵抗値を求めるプログラムを作成してください。
- 入力される値
-
N
s_1 w_1
s_2 w_2
...
s_N w_N
M
t_1 t_2 ... t_M
1 行目には入力される抵抗の種類の総数 N が入力されます。
続く N 行のうち i + 1 行目 (1 ≦ i ≦ N) には、i 番目の抵抗の抵抗名 s_i と抵抗値 w_i が与えられます。
N + 2 行目には与えられる文字列の個数を表す整数 M が与えられます。
N + 3 行目には抵抗のつなぎ方を表す文字列 t_i (1 ≦ i ≦ M) が与えられます。
空白区切りの場合は直列、区切りがない場合は並列でつながれていることを表します。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
回路全体での抵抗値を小数点以下を切り捨てた値を出力してください。
ただし、計算過程では小数点以下を考慮してください。
末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・ 1 ≦ N ≦ 26
・ 1 ≦ w_i ≦ 1000 (1 ≦ i ≦ N)
・ s_i (1 ≦ i ≦ N) は英大文字からなる長さ 1 の文字列
・ s_i ≠ s_j (i ≠ j)
・ 1 ≦ M ≦ 1000
・ t_i (1 ≦ i ≦ M) は s_j (1 ≦ j ≦ N) に登場する文字からなる
・ t_i (1 ≦ i ≦ M) の長さは 1000 以下である
- 入力例1
-
2
A 100
B 200
3
A B B
- 出力例1
-
500
- 入力例2
-
3
A 100
B 200
C 300
2
AB C
- 出力例2
-
366

