部外者をはじけ Objective-C編(paizaランク B 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
あなたはテレビ局の制作スタッフです。
あなたは今ヘリで上空から撮影したとあるイベントの映像を編集しています。
このイベントは参加者が一直線に一本の長い列を作ることで有名です。
あなたはこれを強調するため、映像の列上に赤い直線を引こうとしていますが、1 コマごとに手動で線を引くのが面倒になりました。
実はプログラマーでもあるあなたは、この作業をプログラムで自動化することにしました。
映像から人の座標を検出するプログラムは既にできていますが、いざ直線を引く段階で人の列と引いた直線がずれるバグが発生しました。
どうやら人の座標検出の際に、イベント参加者以外の部外者の座標を同時に検出してしまっていることが原因のようです。
部外者を検出し、バグを取り除くのが今回のミッションです。
ここでは直線から 2 m以上離れた人を部外者として処理することにします。
ある直線を引いた際に最も部外者が少なくなるような直線を、列に対する「正しい直線」とします。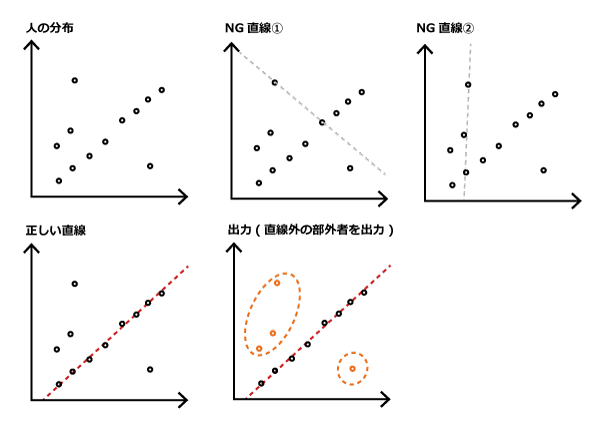
各人物には 1 から N までの番号が振られます。
映像に映った各人物の座標が与えられるので、正しい直線を引いたときの部外者を検出するプログラムを作成しましょう。
人の大きさは考えず、点としてみなしてよいものとします。
また、正しい直線上にいる人物が最低二人以上存在することは保障されています。
また、条件をみたす直線は複数存在する場合がありますが、答えは必ず一意に定まります。
ここで、任意の二点 (x_1, y_1), (x_2, y_2) を結ぶ直線の方程式 ax + by + c = 0 は次のように計算できます。
(y_2-y_1) * x + (x_1-x_2) * y + {(x_2-x_1) * y_1 - (y_2-y_1) * x_1} = 0
また、ある点 (x_i, y_i) と直線 ax + by + c = 0 との距離 d_i は次のように求まります。
d_i = |a * x_i + b * y_i + c| / (a^2 + b^2)^(1/2)
- 入力される値
-
N
x_1 y_1
.
.
.
x_N y_N
・1 行目には、検出した人の数 N が入力されます。
・i+1 (1 ≦ i ≦ N) 行目には、i 番目の人物の二次元座標 (x_i, y_i) が空白区切りで与えられます。
・なお、座標の単位は [m] で、座標はそれぞれ小数点以下 2 桁までの小数で与えられます。
・入力は合計 N + 1 行からなり、末尾に改行を 1 つ含みます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
正しい直線を引いたとき部外者として検出された人物の番号を昇順に改行区切りで出力してください。
部外者が 1 人も存在しなかった場合は文字列noneを出力してください。
出力の末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースで以下の条件を満たします。
・ 2 ≦ N ≦ 100
・ 0 ≦ (部外者の数) < (N/2)
・ 0 ≦ x_i < 640
・ 0 ≦ y_i < 480
・ (x_i,y_i) ≠ (x_j,y_j) (i ≠ j)
- 入力例1
-
20
331.26 330.83
264.31 3.44
118.56 118.09
162.59 162.15
329.92 330.36
271.86 272.05
371.44 371.42
340.22 340.48
286.67 286.36
466.66 466.17
407.49 407.67
381.02 381.45
271.05 270.96
39.97 39.84
464.65 464.65
352.98 352.62
260.1 260.41
31.92 31.92
476.45 139.5
184.83 185.22
- 出力例1
-
2
19
- 入力例2
-
2
210.43 423.86
104.71 212.42
- 出力例2
-
none
- 入力例3
-
4
10.0 20.0
340.0 235.0
20.0 40.0
30.0 60.0
- 出力例3
-
2

