#03:ロジックの概要
このチャプターでは、「長テーブルのうなぎ屋」問題の解法ロジック概要について考え、
日本語で記述をしていきます。いきなりプログラミングを始めずまず処理手順を考えてみましょう。
※本チャプターは動画のみで演習課題はありません。
動画内で解説しているプログラムのロジックを日本語で記述してみましょう。
まずは、大きく入力処理、本処理、出力処理という粒感で考えていくと良いでしょう。
右側のエディタエリアに、日本語でロジックを書いてみましょう。”//”を冒頭に書いて
コメントとして記述していくと、後でプログラミングする際に進めやすくなります。
※この課題は採点されません。
テーブルの様子を配列で表現してみると良いでしょう。
配列のkeyで席番号を、valueで空席状況を表現します。
長テーブルのうなぎ屋
 下記の問題をプログラミングしてください。
下記の問題をプログラミングしてください。
東京の下町に長テーブルで有名な老舗うなぎ屋がありました。
そのうなぎ屋にはとても大きい長テーブルがあり、テーブルの周りにn個の座席が配置されています。
座席には、時計回りに1, 2, …, nと番号が振られています。
座席はテーブルの周りに配置されているので、座席番号nの座席と1の座席は隣接しています。(下記図を参照の事)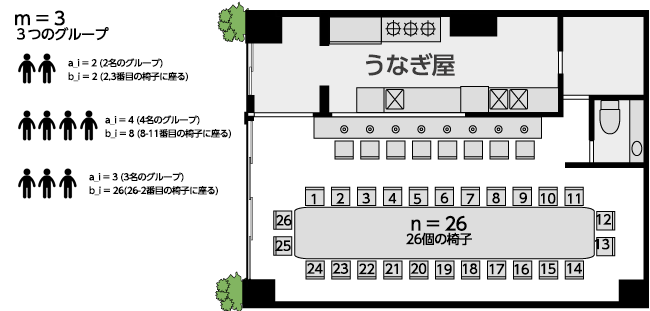
今、m個のグループの人達が座席に順番に座りに来ます。i番目(1≦i≦m)のグループの人数をa_i人とします。
彼らは、長テーブルに並んだ座席の内、ある連続するa_i個の座席に一斉に座ろうとします。
ただしお客さんは江戸っ子なので、それら座席のうち、いずれか一つでも既に先客に座られている座席があった場合、
一人も座らずにグループ全員で怒って帰ってしまいます。江戸っ子は気が早いんでぃ。
入力では、i番目のグループが座ろうとする連続した座席の位置は、整数b_iにより指定されます。
i番目のグループは、座席番号b_iの座席を始点として、そこから時計回りにa_i個分の座席に座ろうとします。
最後のグループが座りに来た後、無事に長テーブルの座席に着席出来ている人数を出力するプログラムを作成してください。
入力される値
入力はm+1行から成ります。
1行目にはn(座席数)とm(グループ数)が半角スペース区切りで入力されます。
i+1行目(1≦i≦m)には2個の整数a_i(グループの人数)とb_i(着席開始座席番号)が半角スペース区切りで入力されます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。
期待する出力
最後のグループが座りに来た後、無事に座席に着席出来ている人数を1行で出力してください。
条件
すべてのテストケースにおいて、入力される値は以下の条件を満たします。
1 ≦ n ≦ 100
1 ≦ m ≦ 100
1 ≦ a_i ≦ n
1 ≦ b_i ≦ n
入力例1
6 3
3 2
1 6
2 5
出力例1
4
入力例2
12 6
4 6
4 8
4 10
4 12
4 2
4 4
出力例2
12