ランク D(Beta)編(paizaランク B 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
この問題では、ユニオン操作に工夫を加えてみましょう。
長さ n の数列 A を考え、数列 A の初期値を [0, 1, ..., n-1] とします。A の i 番目 (0 ≦ i ≦ n-1) の要素 A_i は整数 i の親を表しています。
ここで、ある整数 p の親を順々にたどっていった、p の祖先(または p 自身)である q について、A の q 番目の要素が q であるとき「 p は q の根である」と定義します。つまり、A の初期値では、すべての i (0 ≦ i ≦ n-1) において、i 自身が根となっています。
数列 A に加えて、もう一つ長さ n の数列 R を考え、数列 R の初期値を [1, ..., 1] とします。R の i 番目 (0 ≦ i ≦ n-1) の要素は整数 i のランクをを表しています。ランクとは、整数 i が属する木の、根から末端までの最大の長さのことです。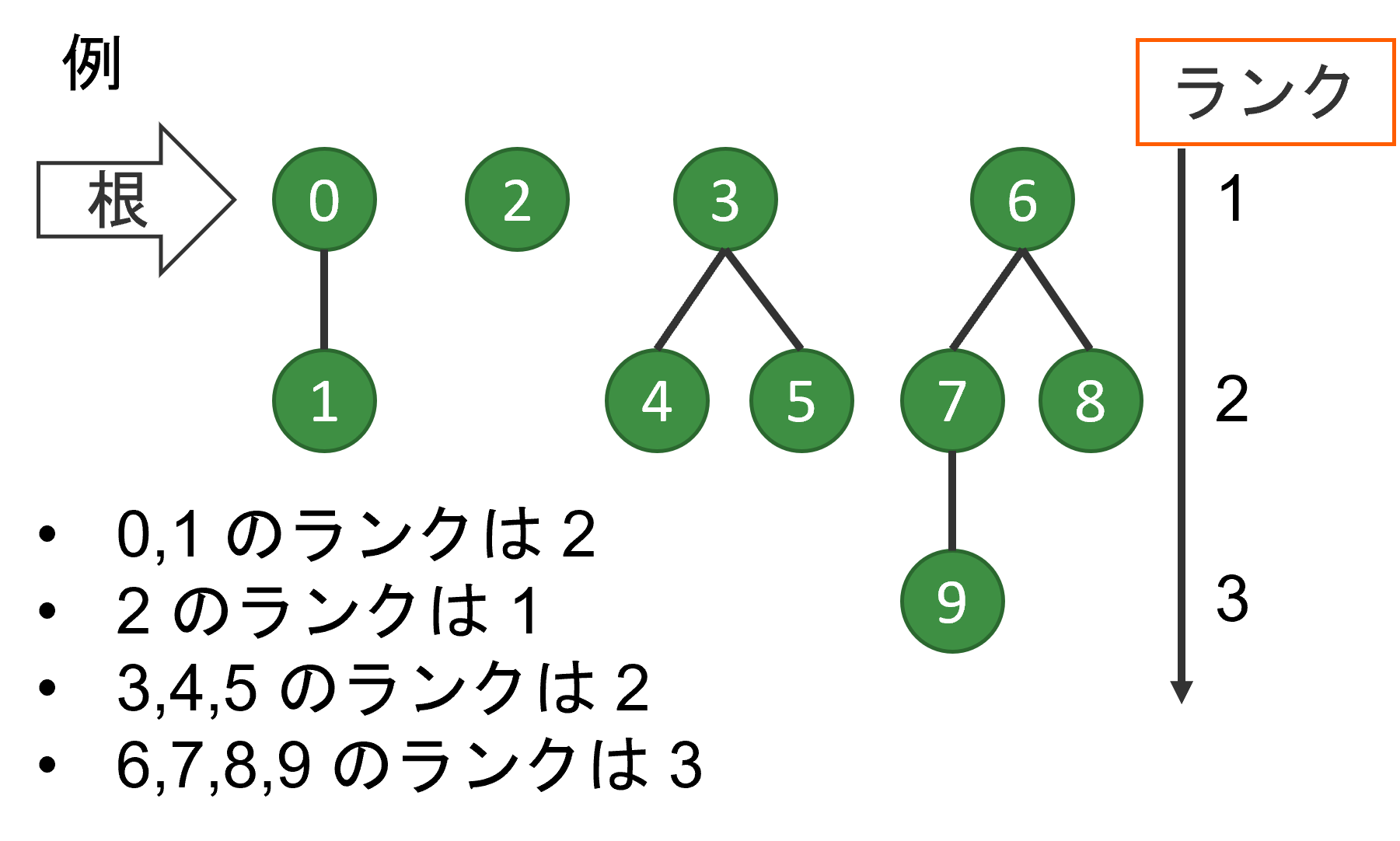
整数の組 (a,b) が合計 q 組与えられます。(a_j, b_j) (1 ≦ j ≦ q) に対して a_j の根を root(a_j)、b_j の根を root(b_j) として、次の操作を与えられた順番に処理し、最後に処理がすべて終了したあとの数列 A を出力してください。
root(a_j) と root(b_j) が同じでないなら、ランクが低いほうの根の親をランクが高いほうの根とする。ランクが同じ場合、root(b_j) の親を root(a_j) の親とする。
root(a_j) と root(b_j) の値が同じならば何もしない。
ただし、p の根 root(p) は、p を入力として root(p) を返す次の関数
improved_find を用いて求めてください。(この関数で求めない場合、処理終了後の数列 A が正しく出力されない可能性があります。)def improved_find(p)
if p == A_p then
return p
else
A_p = improved_find(A_p)
return A_p
end if
- 入力される値
-
n q
a_1 b_1
...
a_q b_q
・ 1 行目に、整数 n と整数 q が半角スペース区切りで与えられます。
・ 1 + j 行目 (1 ≦ j ≦ q) に、整数の組 a_j と b_j が半角スペース区切りで与えられます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
数列 A の i (0 ≦ i ≦ n-1) 番目の要素が i 行目となるように、そして数列 R の i (0 ≦ i ≦ n-1) 番目の要素が n+i 行目となるように、合計 2n 行出力してください。
末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・ 入力はすべて整数
・ 1 ≦ n ≦ 10,000
・ 1 ≦ q ≦ n
・ 0 ≦ a_j, b_j ≦ n-1 (1 ≦ j ≦ q)
・ a_j ≠ b_j (1 ≦ j ≦ q)
- 入力例1
-
6 5
4 5
3 4
2 3
1 2
0 5
- 出力例1
-
4
4
4
4
4
4
1
1
1
1
2
1
- 入力例2
-
10 8
8 9
6 7
7 9
4 5
2 3
3 5
5 9
0 1
- 出力例2
-
0
0
2
2
2
2
2
6
6
6
2
1
4
1
2
1
3
1
2
1

