2-opt法によるTSP (paizaランク S 相当)

問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！

問題

下記の問題をプログラミングしてみよう！

巡回セールスマン問題とは、都市の集合と各都市間の距離が与えられ、全都市をちょうど1回ずつ訪れたのち出発した都市に戻ってくるような経路 (巡回路) のうち最も短いものを求める問題です。

ここでは、2-opt 法と呼ばれるアルゴリズムを学習しましょう。このアルゴリズムは発見的解法 (ヒューリスティクス) と呼ばれるもので、ある程度良い解が出力されることが期待されるものの、解の精度は全く保証されません。

2-opt 法の概要は、以下の通りです。

・ 巡回路を適当に作り、初期解とする
・ 一定の回数か、解があまり改善されなくなるまで以下を繰り返す
    ・ (*) 巡回路を成す辺を 2 本選び、その辺を繋ぎ変えることを考える。繋ぎ変えることによって巡回路長が短くなるなら繋ぎ変える。短くならないなら何もしない

例えば、下図ではdist(a, d) + dist(b, c) > dist(a, b) + dist(c, d)が成り立つため、辺を繋ぎ変えます。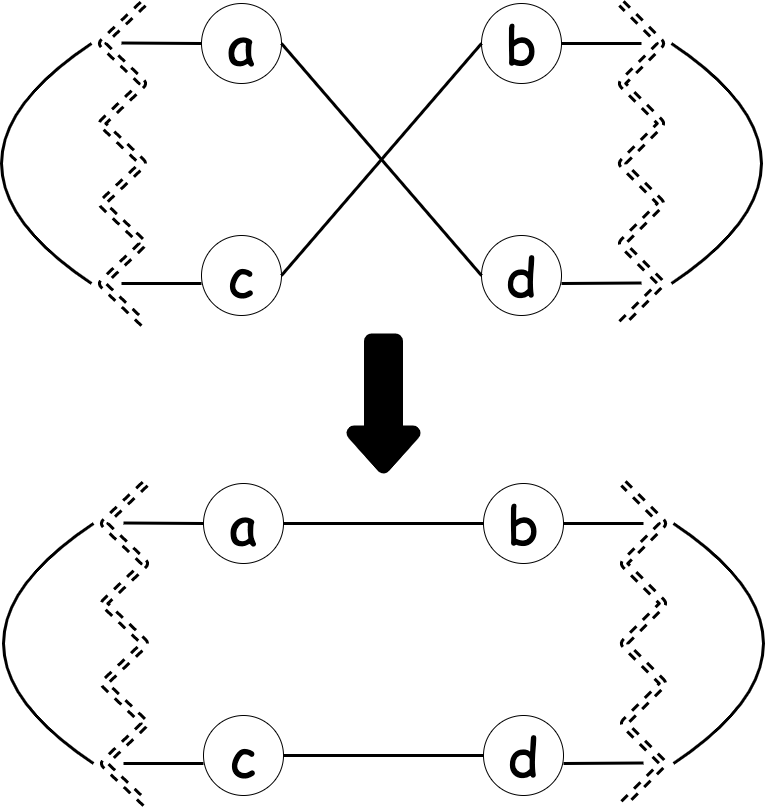

n 個の都市 (都市 0、都市 1、...、都市 n-1) のデータと、n 個の都市を巡る初期巡回路、整数 q が与えられます。2-opt 法を実装し、巡回路を求めてください。(*) の処理は q 回繰り返してください。

ジャッジの都合上で解を一意にするために、辺を 2 本選ぶ際には以下で指定する疑似乱数生成プロシージャ (xorshift32) を用いてください。(unsigned int は符号なし 32 bit 整数型)

unsigned int state = 813;

unsigned int xorshift32(){
    unsigned int x = state;
    x ^= x << 13;
    x ^= x >> 17;
    x ^= x << 5;
    state = x;
    return state;
}

void pick_two(int &a, int &b){
    while(true){
        a = xorshift32()%n;
        b = xorshift32()%n;
        if(a > b){
            swap(a, b);
        }
        if(!(a+1 < b) || (a == 0 && b == n-1)){
            continue;
        }
        return;
    }
}

2-opt 法の疑似コードを以下に示します。なお、SWAP(a, d, b, c)は巡回路 tour の辺 (a, d) と (b, c) を繋ぎ変えて辺 (a, b) と (c, d) にする処理を表します。

void two_opt(int tour[], int q){
    for(int i = 0; i < q; i++){
        int a, b;
        pick_two(a, b);

        d_before = (現在の巡回路 tour の巡回路長)
        d_after = (現在の巡回路 tour の都市 tour[a] と tour[(a+1)%n] を結ぶ辺と、都市 tour[b] と tour[(b+1)%n] を結ぶ辺を繋ぎ変えた巡回路の巡回路長)

        if(d_after < d_before){
            // 辺を繋ぎ変え巡回路を更新する
            SWAP(tour[a], tour[a+1], tour[b], tour[(b + 1)%n]);
        }
    }
}

なお、各都市は二次元平面上の点として与えられ、都市間の距離にはユークリッド距離を用いるものとします。

巡回路の始点は任意です。巡回路が正しければ正解と判定されます。

入力される値

n q
x_0 y_0
x_1 y_1
...
x_{n-1} y_{n-1}
p_0
p_1
...
p_{n-1}

・ 1 行目に、都市の個数 n と整数 q が与えられます。
・ 2 行目から、n 行にわたり n 個の都市の座標が与えられます。
・ n+2 行目から、n 行にわたり初期巡回路が与えられます。

入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。標準入力からの値取得方法はこちらをご確認ください

期待する出力: 出力は n 行になります。(*) の処理を q 回繰り返した結果得られる巡回路を出力してください。巡回路は都市番号 (0, 1, ... , n-1) の順列で表し、都市番号を先頭から順に各行に 1 つずつ出力してください。

条件: すべてのテストケースにおいて、以下の条件をみたします。
・入力はすべて整数
・ 100 ≦ n ≦ 3,000
・ 100 ≦ q ≦ 3,000
・ -1,000 ≦ x_i, y_i ≦ 1,000 (0 ≦ i ≦ n-1)
・ i ≠ j ならば (x_i, y_i) ≠ (x_j, y_j)
・ p は {0, 1, ... , n-1} を並べ替えた順列

入力例1: 100 2303
-903 604
758 98
489 -60
155 480
-582 650
963 -868
988 -989
-689 305
896 -560
212 135
-901 333
-967 485
-470 -462
186 314
-73 -309
-973 -244
463 691
-286 365
46 526
293 -161
571 837
398 -992
124 -606
-379 335
-540 -844
853 504
-711 465
-458 717
434 -757
-952 304
254 575
360 644
-912 -43
-712 262
45 -798
-161 296
-859 -274
-101 590
-678 171
219 334
-207 447
241 535
256 -27
560 -926
-272 214
-533 480
-598 -683
757 -233
94 381
105 931
-142 398
-782 271
-454 -210
436 -833
369 -298
956 612
-133 937
-421 -600
-506 21
409 481
910 -646
427 -594
84 -793
732 384
40 611
-82 -207
5 580
-861 -261
937 -466
211 619
203 -689
912 736
-646 -169
750 311
334 0
862 -871
289 -254
-530 -355
242 -203
-59 551
637 -209
291 150
-595 204
-229 -446
729 343
158 -893
987 -817
564 -219
248 928
685 -46
90 -300
288 46
129 -362
-245 615
-801 -213
-420 431
-521 558
-876 645
551 -749
-540 -855
88
20
72
38
98
10
2
48
50
62
32
58
29
47
70
42
24
81
78
4
17
94
53
76
45
89
26
22
95
66
84
46
41
27
6
85
11
77
14
37
69
60
55
86
96
3
99
91
18
57
74
44
67
8
34
59
40
82
15
49
19
64
75
9
1
16
33
80
87
12
21
39
43
90
83
92
54
93
23
30
61
35
13
28
25
79
56
68
73
71
65
63
5
52
36
31
7
97
51
0

出力例1: 88
69
30
41
59
31
20
71
55
25
16
73
63
1
84
68
60
98
43
8
89
2
74
14
65
90
91
42
34
57
12
52
58
33
7
17
40
45
96
4
27
93
11
0
97
29
10
26
51
94
72
38
82
23
50
95
35
44
66
37
32
15
36
67
99
24
46
77
83
70
22
28
75
6
5
86
61
92
62
85
21
53
78
19
76
54
87
80
47
81
9
13
18
39
79
64
3
48
49
56

問題一覧へ戻る