辺の交換 Clojure(Beta)編（paizaランク A 相当）

問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！

問題

下記の問題をプログラミングしてみよう！

巡回セールスマン問題とは、都市の集合と各都市間の距離が与えられ、全都市をちょうど1回ずつ訪れたのち出発した都市に戻ってくるような経路 (巡回路) のうち最も短いものを求める問題です。

ここでは、2-opt 法と呼ばれるアルゴリズムを学習しましょう。このアルゴリズムは発見的解法 (ヒューリスティクス) と呼ばれるもので、ある程度良い解が出力されることが期待されるものの、解の精度は全く保証されません。

2-opt 法の概要は、以下の通りです。

・ 巡回路を適当に作り、初期解とする
・ 一定の回数か、解があまり改善されなくなるまで以下を繰り返す
    ・ 巡回路を成す辺を 2 本選び、その辺をつなぎ変えることを考える。つなぎ変えることによって巡回路長が短くなるならつなぎ変える。短くならないなら何もしない

例えば、下図ではdist(a, d) + dist(b, c) > dist(a, b) + dist(c, d)が成り立つため、辺をつなぎ変えます。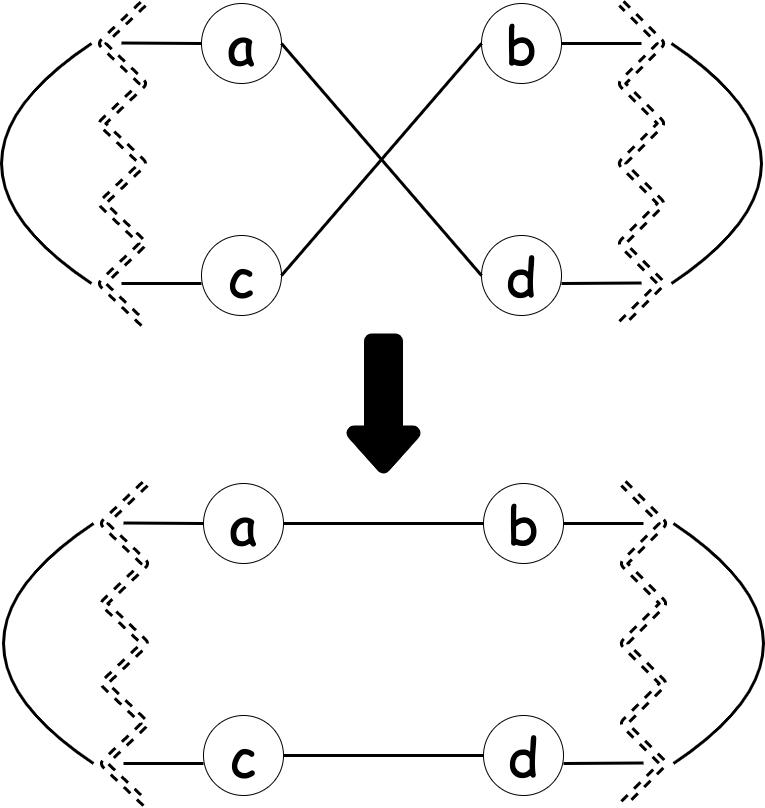

ここでは、この 2-opt 法を実装する前準備として、辺をつなぎ変える練習をしましょう。

n 個の都市のデータ (都市 0、都市 1、...、都市 n-1) と、n 個の都市を巡る巡回路と、その巡回路上の辺 2 本が与えられます。辺をつなぎ変えることによって巡回路長が短くなる場合は 1 行目にYesと出力し、2 行目以降に辺をつなぎ変えた巡回路を出力してください。短くならない場合は 1 行目にNoと出力してください。
なお、各都市は二次元平面上の点として与えられ、都市間の距離にはユークリッド距離を用いるものとします。

巡回路の始点は任意です。巡回路が正しければ正答と判定されます。

入力される値

n
x_0 y_0
x_1 y_1
...
x_{n-1} y_{n-1}
p_0
p_1
...
p_{n-1}
a b

・ 1 行目に、都市の個数 n が与えられます。
・ 2 行目から、n 行にわたり n 個の都市の座標が与えられます。
・ n+2 行目から、n 行にわたり初期巡回路が与えられます。
・ 2n+2 行目に、2 本の辺の始点を表す整数 a, b が与えられます。2 本の辺は、都市 p_a と p_{(a+1)%n} を結ぶ辺と、都市 p_b と p_{(b+1)%n} を結ぶ辺です。

入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。標準入力からの値取得方法はこちらをご確認ください

期待する出力: 出力は n+1 行または 1 行です。辺をつなぎ変えることによって巡回路長が短くなる場合は 1 行目にYesと出力し、2 行目以降に辺をつなぎ変えた巡回路を出力してください。巡回路は都市番号 (0, 1, ... , n-1) の順列で表し、都市番号を先頭から順に各行に 1 つずつ出力してください。辺をつなぎ変えても巡回路長が短くならない場合は 1 行にNoと出力してください。

条件: すべてのテストケースにおいて、以下の条件をみたします。
・入力はすべて整数
・ 4 ≦ n ≦ 3,000
・ -1,000 ≦ x_i, y_i ≦ 1,000 (0 ≦ i ≦ n-1)
・ i ≠ j ならば (x_i, y_i) ≠ (x_j, y_j)
・ p は {0, 1, ... , n-1} を並べ替えた順列
・ 0 ≦ a < b ≦ n-1
・ a+1 < b
・ a = 0 のとき、b != n-1

入力例1: 4
0 0
2 2
-1 1
1 -1
1
2
3
0
1 3

出力例1: Yes
0
2
1
3

入力例2: 4
0 0
2 2
-1 1
1 -1
1
3
0
2
0 2

出力例2: No

問題一覧へ戻る