子の頂点 Java編(paizaランク C 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
このチャプターでは、グラフ理論における二分木よりもさらに分岐の多い木(多分木以上)を扱います。
二分木と同様に、子は「左から i 番目の子」と行った具合に区別することができます。
例として、A は B と C と D の親、 B は A の左から 1 番目の子、 C は A の左からの 2 番目の子、 D は A の左からの 3 番目の子であるような関係を図に起こすと下のようになります。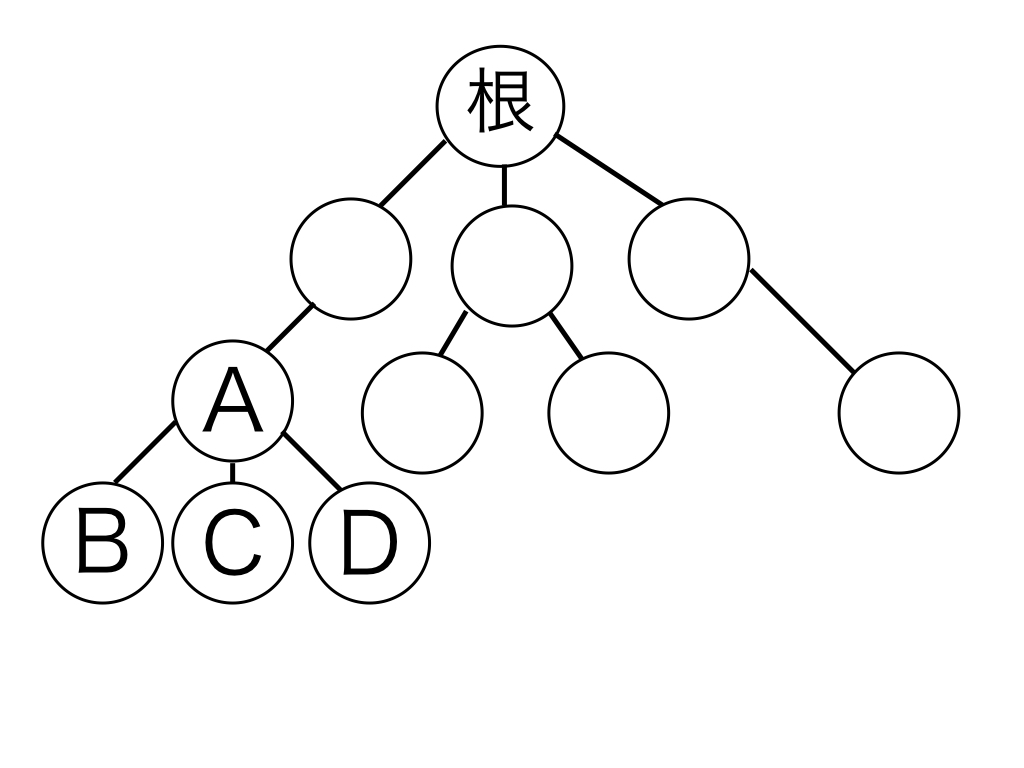
このような木の頂点や辺を子の左右の区別がわかる形式で管理するには、普通の木と同様に隣接行列や隣接リストで管理するだけでは足りません。各頂点について構造体を用意したり、頂点自体に左右の特性づけを行うなど、管理方法を工夫する必要があります。
三分木以上の分岐を持つ木の頂点・辺についての情報と K 個の頂点と左から何番目の子を求めたいのかが与えられるので、与えられた各頂点の指定された子の頂点番号を出力してください。
なお、今回の問題では、子の順番は入力された順に左から順序付いているものとします。
- 入力される値
-
N K R
a_1 b_1
...
a_{N-1} b_{N-1}
v_1 l_1
...
v_K l_K
・1 行目には、根付き木の頂点の数 N, 与えられる頂点の数 K, 多分木の根の頂点番号 Rが与えられます。
・続く N-1 行では、根付き木の各辺の両端の頂点 a_i , b_i が与えられます。ただし、a_i は b_i の親であることが保証されています。(1 ≦ i ≦ N-1)
・続く K 行では、子の頂点を求めたい頂点の番号 v_i と調べたい子の左からの順番 l_i が与えられます。(1 ≦ i ≦ K)
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
・合計で K 行出力してください。
・i 行目では、v_i の左から l_i 番目の子の頂点番号を出力してください。(1 ≦ i ≦ K)
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・1 ≦ N ≦ 100
・1 ≦ K ≦ 100
・1 ≦ R ≦ N
・1 ≦ a_i , b_i ≦ N (1 ≦ i ≦ N-1)
・1 ≦ v_i ≦ N (1 ≦ i ≦ K)
・1 ≦ l_i ≦ 頂点 v_i の子の数(1 ≦ i ≦ K)
- 入力例1
-
10 3 4
10 7
7 2
2 8
4 10
10 1
4 5
7 6
8 3
4 9
7 1
10 2
7 1
- 出力例1
-
2
1
2
- 入力例2
-
20 6 2
20 14
4 20
14 17
11 4
19 11
2 19
4 1
17 7
7 13
1 5
17 12
19 16
16 10
2 3
20 9
3 15
3 8
12 18
11 6
2 2
11 2
1 1
4 2
17 2
4 1
- 出力例2
-
3
6
5
1
12
20

