木の入力の受け取り（隣接行列） Clojure(Beta)編（paizaランク D 相当）

この問題集では、グラフ理論における木を扱います。
木とは、n 個の頂点と、それら全てを連結する n-1 個の辺からなるグラフのことです。
例として、以下の図 1 は頂点数が 5 の木ですが、辺の数が 5 である図 2 と、5 つの頂点全てを連結していない図 3 は木ではありません。

図 1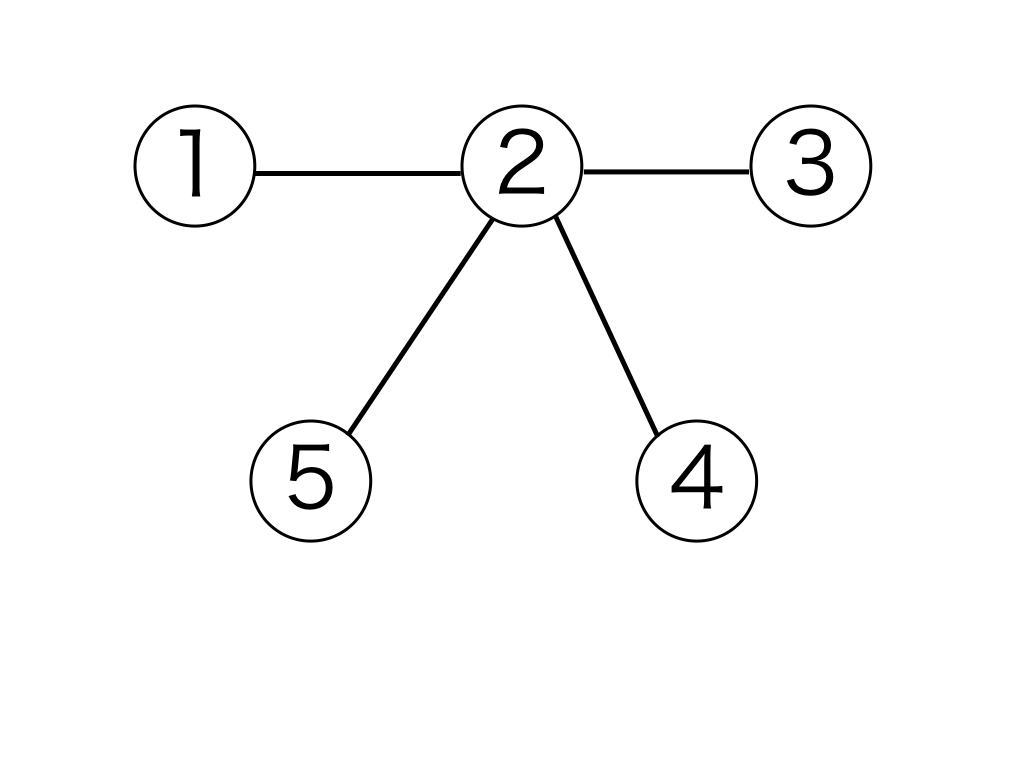

図 2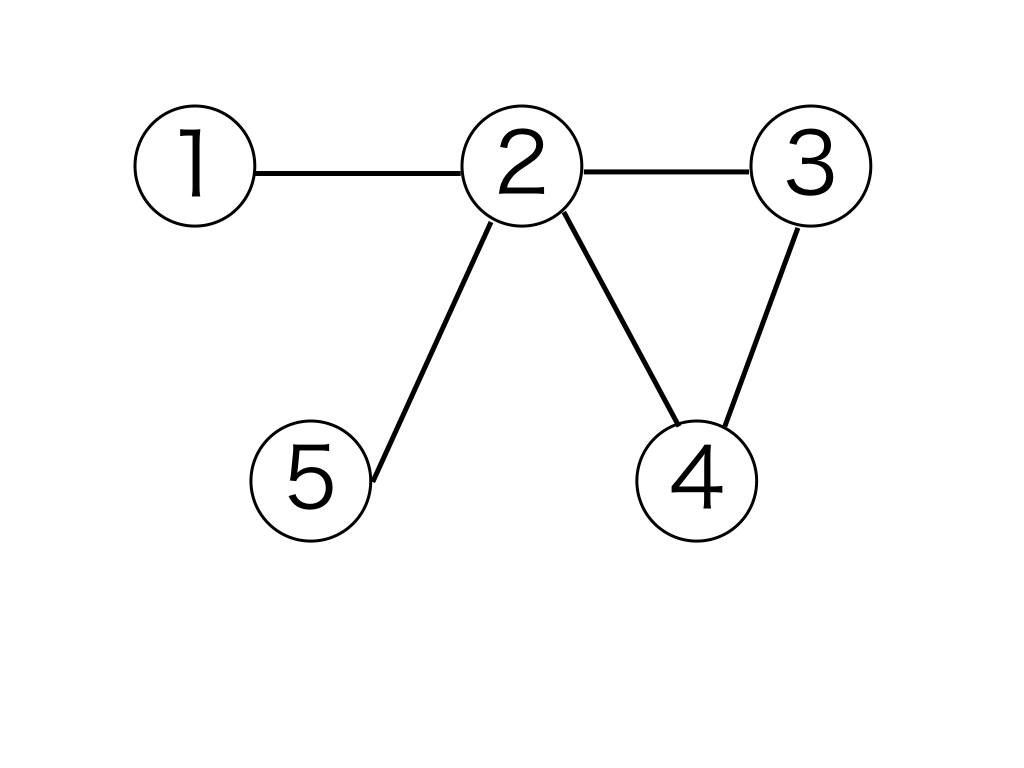

図 3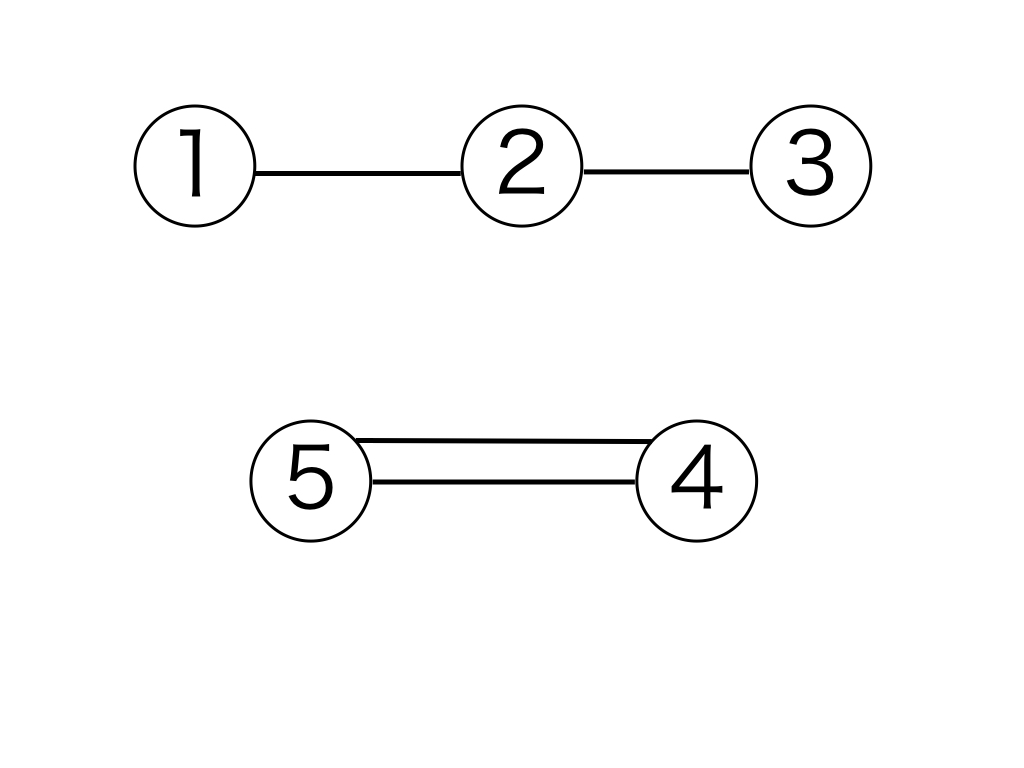


プログラミングで木を扱う際には、辺の情報を利用しやすい形で保持することが好まれるので、隣接行列や隣接リストと呼ばれる形式で辺の情報を管理します。
この問題では、隣接行列を用いて辺の情報を管理してみましょう。

グラフ (頂点数 N) の隣接行列とは、 N × N の行列 g であって i 行 j 列目の要素が
・ i 番目の頂点と j 番目の頂点が辺で結ばれているとき 1
・ 結ばれていないとき 0
であるようなもののことをいいます。

木の頂点・辺についての情報が与えられるので、この木の隣接行列を出力してください。