部分和問題 Elixir(Beta)編（paizaランク B 相当）

長さ N の数列 a_1, a_2, ..., a_N と正の整数 K が与えられます。
a_1, a_2, ..., a_N からいくつかの要素を選んでその和を K とすることはできるかを判定してください。
ただし、1 つも選ばないときの和は 0 とします。
できるなら Yes、できないなら No を出力してください。


・ヒント 1 : 全探索を行う
長さ N の 数列 a_1, a_2, ..., a_N があるときそこから要素を選ぶ組み合わせは 2^N 通りあります。
この問題で与えられる最大の N は 20 となるため、最大で 2^20 = 1048576 ≒ 10^6 通りです。
この組み合わせを全て試しても実行時間制限には間に合うため、全ての組み合わせを実際に試します。

・ヒント 2 : ビット全探索
ヒント 1 の全ての組み合わせを試す方法には深さ優先探索、幅優先探索、ビット全探索などが考えられます。
この問題ではビット全探索を用いることとします。ビット全探索は数値の 2 進数表現を用いた探索方法です。
下に示すのは 0 から 7 までの数値を N=3 ビットの 2 進数で表した表です。
ここで「a_i (1 ≤ i ≤ N) 番目を選ぶか」をそれぞれ右から i 番目のビットの 1 (選ぶ) と 0 (選ばない) に対応させると、N=3 の場合の 8 通りの全ての組み合わせ方を網羅できることが分かります。他の N の場合も同様です。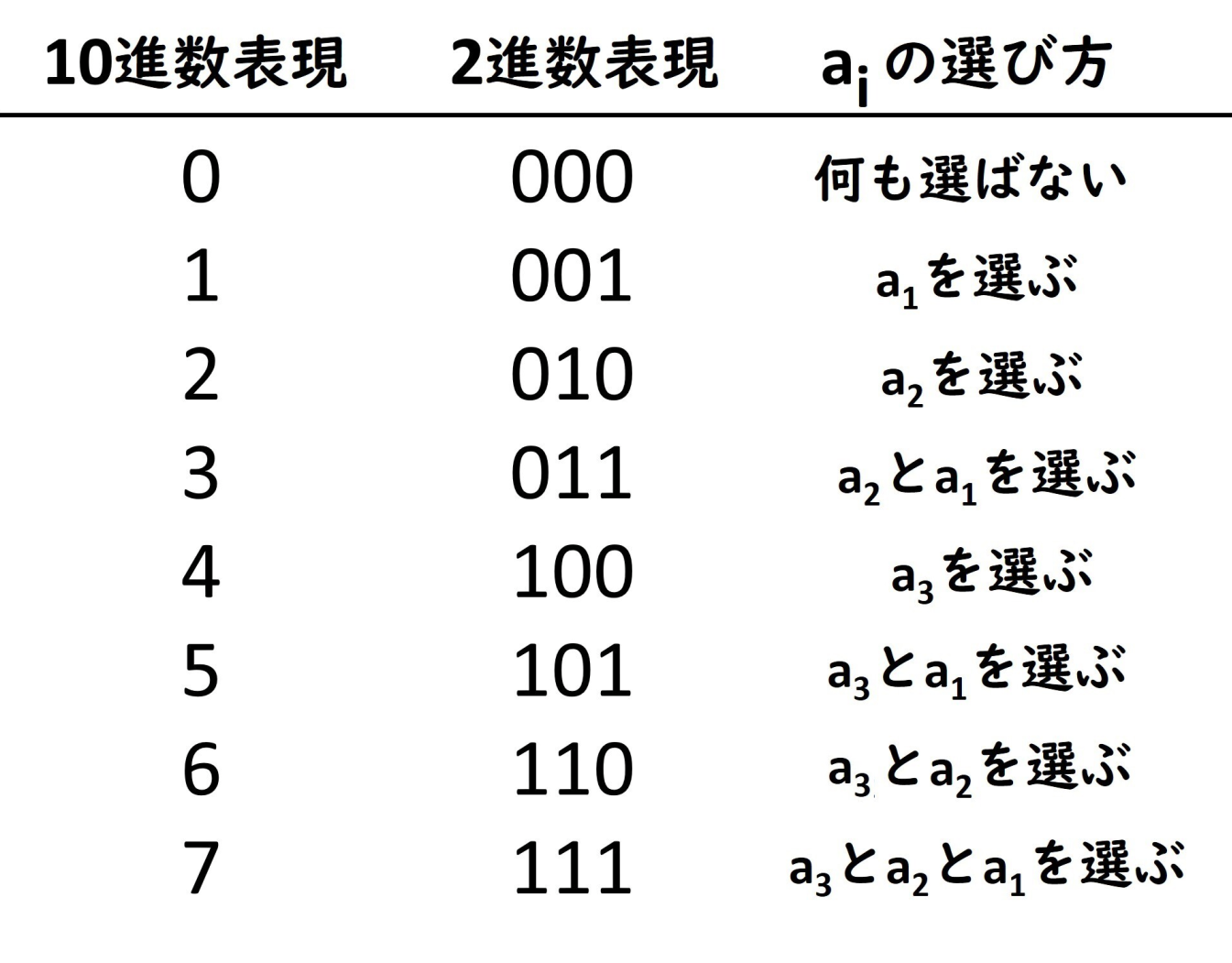





下に C++ と Python それぞれで N=3 のときの 10 進数表現とその 2 進数表現を出力するサンプルコードがあります。
このコードを改変することでこの問題を解くことができます。

サンプルコードの実行結果
num=0 binary=000
num=1 binary=001
num=2 binary=010
num=3 binary=011
num=4 binary=100
num=5 binary=101
num=6 binary=110
num=7 binary=111

//C++のサンプルコード
 #include<iostream>
 #include<vector>
using namespace std;

int main()
{
    int N = 3;
    for (int num = 0; num < (1 << N); ++num)
    {
        string binary = "";
        for (int bit = N - 1; 0 <= bit; --bit)
        {
            //2進数の下からbit桁目が0かをis_oneに格納する
            bool is_one = (1 << bit) & num; 
            //is_oneの値を文字列としてbinaryに付け足す
            binary += is_one ? '1' : '0'; 
        }
        //元の数値numとその2進数表現binaryを出力する
        cout << "num=" << num << " binary=" << binary << endl;
    }
}

#Python3のサンプルコード
N = 3
for num in range(1<<N):
    binary = ""
    for bit in reversed(range(0, N)):
        #2進数の下からbit桁目が0かをis_oneに格納する
        is_one = (1<<bit) & num
        #is_oneの値を文字列としてbinaryに付け足す
        binary += '1' if is_one else '0'
        
    #元の数値numとその2進数表現binaryを出力する
    print("num={} binary={}".format(num, binary))