(問題 7)Segment Treeの区間計算1 : インデックス計算 Haskell(Beta)編（paizaランク A 相当）

(はじめに)

問題 5,6 でSegment Treeの更新についてやってきました。

最後に、問題 7,8,9 を通してSegment Treeを用いて区間クエリ(ここでは区間max)を処理していきます。

class SegTree():
    def calc(self,a, b): #行いたい処理
        return max(a, b)

    def e(self): #単位元
        return 0

    def __init__(self, n, A):
        #完全2分木を作る
        #N = 2 ** k ≧ n となるようにする。(葉の数がnより多くなるようにする。)
        self.k = (n - 1).bit_length() #bit_lengthメソッドにより取得が出来る。
        N = 2 ** (self.k)
        self.N = N
        self.Tree = [self.e()] * (2 * N - 1)
        #葉の部分に初期要素を入れる
        for i in range(n):
            self.Tree[N - 1 + i] = A[i]
        #葉から近い順にそれぞれの葉以外の頂点の計算を行う
        for i in range(N - 2, -1, -1):
            self.Tree[i] = self.calc(self.Tree[2 * i + 1], self.Tree[2 * i + 2]) #頂点iの子は2i+1,2i+2、そこの2つを用いて計算を行う

    def renewal(self, ind, x): #A[ind]をxに更新
        T = self.N - 1 + ind #A[ind]に対応する場所
        self.Tree[T] = x
        while T > 0: #根にたどるまで更新を続ける
            T = (T - 1) // 2
            self.Tree[T] = self.calc(self.Tree[2 * T + 1], self.Tree[2 * T + 2])

    def product(self, l, r): #A[l]からA[r]までの計算結果を返す
        #問題 7,8,9 で実装

区間クエリにそれぞれ一つずつ計算していく方法では最悪計算量が O(Qn) (Q はクエリ数、n は配列の長さ) になってしまいます。

ここで、事前計算したSegment Treeを用いて O(Q log n) で計算する方法をやっていきます。

そのためには、どこにどのデータが入っているかがわからなければいけません。

今回はそのインデックス計算についてやっていきます。

構築のときにも触れましたが、葉には配列の要素または単位元が入っており、その他の頂点には、2 つの子の計算結果が入っています。

ここで、わかりやすくするため頂点 N - 1 + i に入っているデータを S_i とし、S_[l,r] を S_l,S_{l+1},...,S_r までの計算結果とします。

逆の観点から考えていきます。上記の方法で構築したあと、根である頂点 0 には S_[0,N-1] つまり、すべての葉に対する計算結果が入っています。

そして、それぞれの頂点 i に対し、2 つの子には左の子には頂点 i の前半部分、右の子には頂点 i の後半部分の計算結果が入っています。

以下が N = 8 のときの例です。



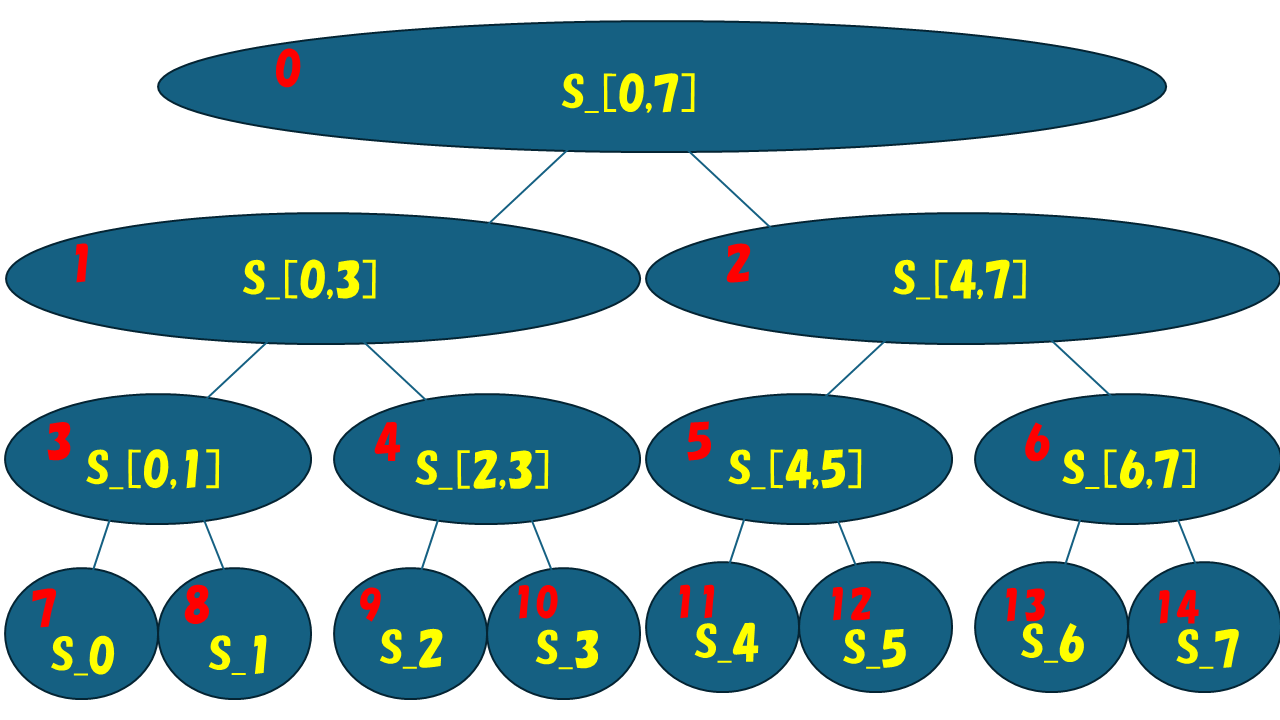
この例をもとに説明すると、頂点 0 には S_0,S_1,...,S_7 に対する計算結果が入っており、その子である頂点 1 には頂点 0 の前半部分、つまり、S_0,S_1,S_2,S_3 に対する計算結果が頂点 2 には頂点 0 の後半部分、つまり、S_4,S_5,S_6,S_7 に対する計算結果が入っています。

ここから、インデックス計算について考えていきます。

根からの距離が k' (≦ k) である頂点の中で最も左にある頂点の番号を考えます。ここで k は木の深さです。

根からの距離が k' 未満の頂点からなる部分グラフも完全二分木になります。したがって、根からの距離が k' である頂点の中で最も左にある頂点は頂点 (部分グラフの頂点数) = 2 ^ k' - 1 と計算できます。

また、いくつの要素の計算結果が根からの距離が k' である頂点に入っているかについては、根にはすべての 2 ^ k 個の要素に対する計算結果が入っており、根からの距離が 1 増えるごとに半分になっていくので 2 ^ (k - k') 個の要素に対する計算結果が入っています。

最後に根からの距離が k' である他の頂点についてですが、それぞれに 2 ^ (k - k') 個の要素に対する計算結果が入っているので、左から、S_[0,2 ^ (k - k') - 1],S_[2 ^ (k - k'), 2 × 2 ^ (k - k') - 1],S_[2 × 2 ^ (k - k'), 3 × 2 ^ (k - k') - 1],...と順に入っていることがわかります。

先ほどの例では頂点 5 には根からの距離が 2 で左から 3 番目の頂点なので、S_[2 × 2 ^ (3 - 2),3 × 2 ^ (3 - 2) - 1] = S_[4,5] が入っていることがわかります。

では以下の問題では p,l に対し、S_[p,p + 2 ^ l - 1] がどこに入っているのかここまでのことを踏まえて計算を行ってみましょう。

(ヒント)まず、2 ^ l = 2 ^ (k - k') を満たす k' を計算してみましょう。それができると、左から何番目であるかも求めることが出来ます。

(問題)

Q 個のクエリが与えられるので順番に処理を行ってください。i 番目のクエリは以下の通りです。

配列の長さが 2 ^ k_i である配列 A に対し、問題 3 の手順でSegment Treeを構築した。A_{p_i} から A_{p_i + 2 ^ l_i - 1} までの計算結果が入っている頂点番号を出力する。