(問題 5)Segment Treeの更新1 : インデックス計算 Python2編（paizaランク B 相当）

(はじめに)

問題 4 まででSegment Treeの構築をしてきました。

ここでは、問題 5,6 でSegment Treeの更新を行っていきます。

class SegTree():
    def calc(self,a, b): #行いたい処理
        return max(a, b)

    def e(self): #単位元
        return 0

    def __init__(self, n, A):
        #完全2分木を作る
        #N = 2 ** k ≧ n となるようにする。(葉の数がnより多くなるようにする。)
        self.k = (n - 1).bit_length() #bit_lengthメソッドにより取得が出来る。
        N = 2 ** (self.k)
        self.N = N
        self.Tree = [self.e()] * (2 * N - 1)
        #葉の部分に初期要素を入れる
        for i in range(n):
            self.Tree[N - 1 + i] = A[i]
        #葉から近い順にそれぞれの葉以外の頂点の計算を行う
        for i in range(N - 2, -1, -1):
            self.Tree[i] = self.calc(self.Tree[2 * i + 1], self.Tree[2 * i + 2]) #頂点iの子は2i+1,2i+2、そこの2つを用いて計算を行う

    def renewal(self, ind, x): #A[ind]をxに更新
        #問題 5,6 で実装

    def product(self, l, r): #A[l]からA[r]までの計算結果を返す
        #問題 7,8,9 で実装

一点更新とは、配列のある要素を特定の値に更新することを意味します。

ここで問題 3 の配列の長さが n = 5 で A = [1,5,7,9,8] のSegment Treeを再掲載します。



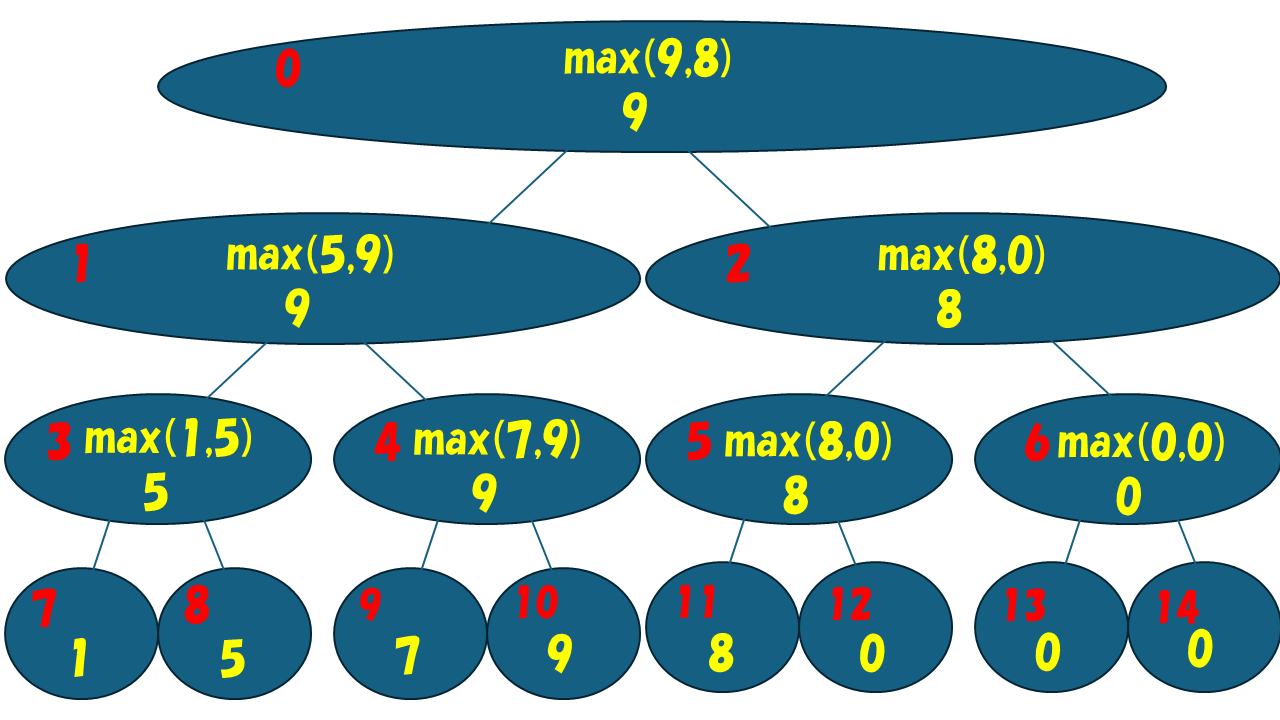
ここでは、A の 3 番目の要素である 9 を 6 にかえることを考えます。

そのとき、この変更がSegment Treeに与える影響について見ていきましょう。

A の 3 番目の要素に対応するSegment Treeの頂点 10 に乗っているデータが 9 から 6 に更新されます。

他の葉については更新する必要がありません。他の頂点について見ていきましょう。

ここで、頂点 i に乗っているデータを T_i とします。更新された T_10 が計算対象に含まれている、またその時に限って、そのデータも更新する必要があります。

頂点 6 : T_13 と T_14 の最大値 → T_10 を含んでいないため更新する必要なし

頂点 5 : T_11 と T_12 の最大値 → T_10 を含んでいないため更新する必要なし

頂点 4 : T_9 と T_10 の最大値 → T_10 を含んでいるため更新する必要あり

頂点 3 : T_7 と T_8の最大値 → T_10 を含んでいないため更新する必要なし

頂点 2 : T_5 と T_6 の最大値 → T_11 と T_12 と T_13 と T_14 の最大値 → T_10 を含んでいないため更新する必要なし

頂点 1 : T_3 と T_4 の最大値 → T_7 と T_8 と T_9 と T_10 の最大値 → T_10 を含んでいる更新する必要あり

頂点 0 : T_1 と T_2 の最大値 → T_7 と T_8 と T_9 と T_10 と T_11 と T_12 と T_13 と T_14 の最大値 → T_10 を含んでいる更新する必要あり

よって更新する必要のある頂点を緑で塗りなおした木が以下のようになります。



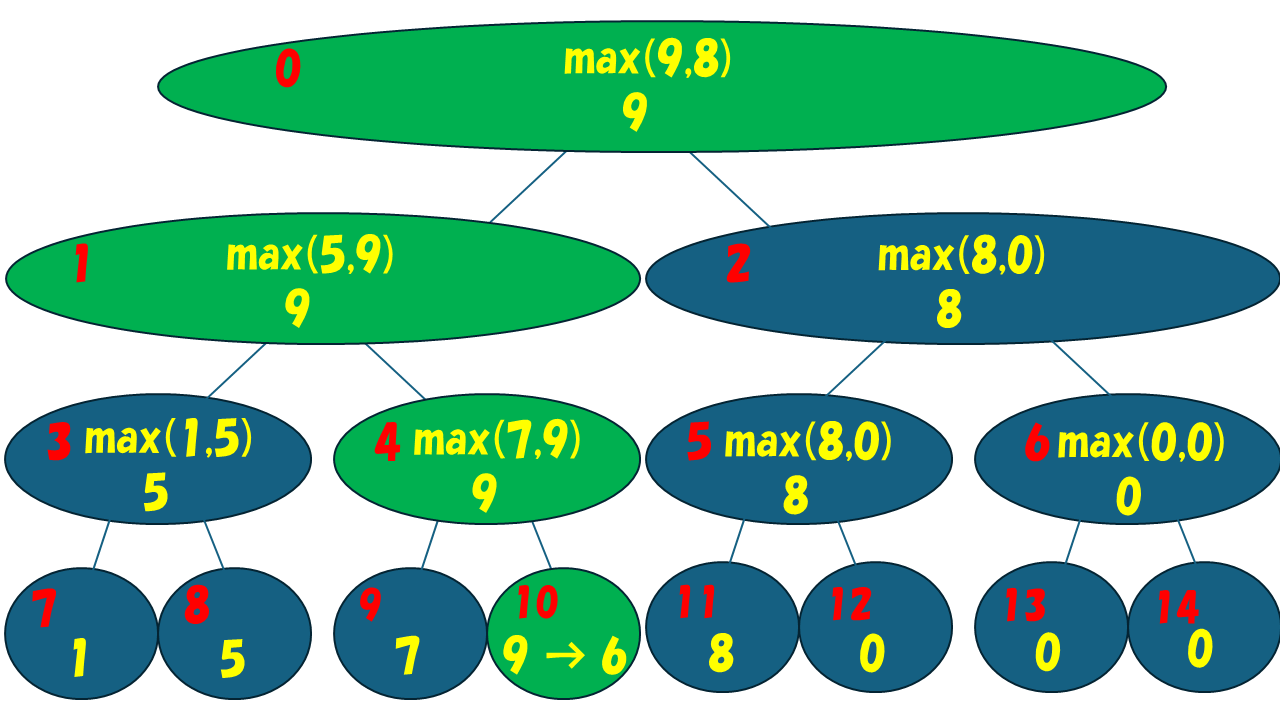
これを見ると、更新対象の葉と根の最短パス上の頂点のみを更新すればいいことがわかります。

同様に考えると他のSegment Treeの更新についても、同様のことが言えます。

では、ここでは与えられた頂点と根の最短パス上の頂点のインデックス計算を問題として取り組んでいきます。

(ヒント) 与えられた頂点から、「親を計算しその頂点に移動する」という処理を根にたどり着くまで繰り返すことで、今回の問題を解くことが出来ます。子の頂点のインデックスが与えられたときに親の頂点のインデックスをもとめる計算方法について考えてみましょう。

(問題)

根が頂点 0 であり、頂点 i (0 ≦ i ≦ 2 ^ 100 - 2) の左の子が頂点 2 × i + 1、右の子が頂点 2 × i + 2 である完全二分木があります。

整数 T が与えられるので、頂点 T と根の最短パス上の頂点を頂点番号の降順にすべて出力してください。