(問題 3)Segment Treeの構築3: Segment Treeの構築 JavaScript編（paizaランク A 相当）

(はじめに)

いよいよ、問題 2 で扱った完全二分木のノードにデータを載せて、演算を高速に処理していきます。

今回は行いたい処理は長さ n = 5 の配列 A = [1,5,7,9,8] に対し、区間maxを計算することを考えていきます。

ここで区間maxとはある範囲における最大値を指します。例えば A の 0 番目から 2 番目までの区間maxは max(1, 5, 7) = 7 となります。

完全二分木に載せるためには葉の数が配列の長さ以上ある必要があります。根と葉の距離を k としたときに、葉の数は 2 ** k となります。そのため、2 ** k ≧ n を満たす必要があります。

また k が大きくなりすぎると、木も大きくなりすぎてしまうためここでは、k は n - 1 のビット長とします。ここでは、0 のビット長は 0 とします。また、葉の数を N = 2 ** k とします。このとき頂点数は 2 × N - 1 とします。

まず、わかりやすくするため完全二分木の各頂点について番号を振っていきます。いろいろな振り方がありますが、実装上以下のルールにのっとって番号を振っていきます。

根を頂点番号 0 とし、頂点 i の左の子が頂点 2 × i + 1, 右の子が頂点 2 × i + 2 となるように番号を振っていきます。

今回、番号を振り終えたものが下の木になります。赤い数字が頂点番号です。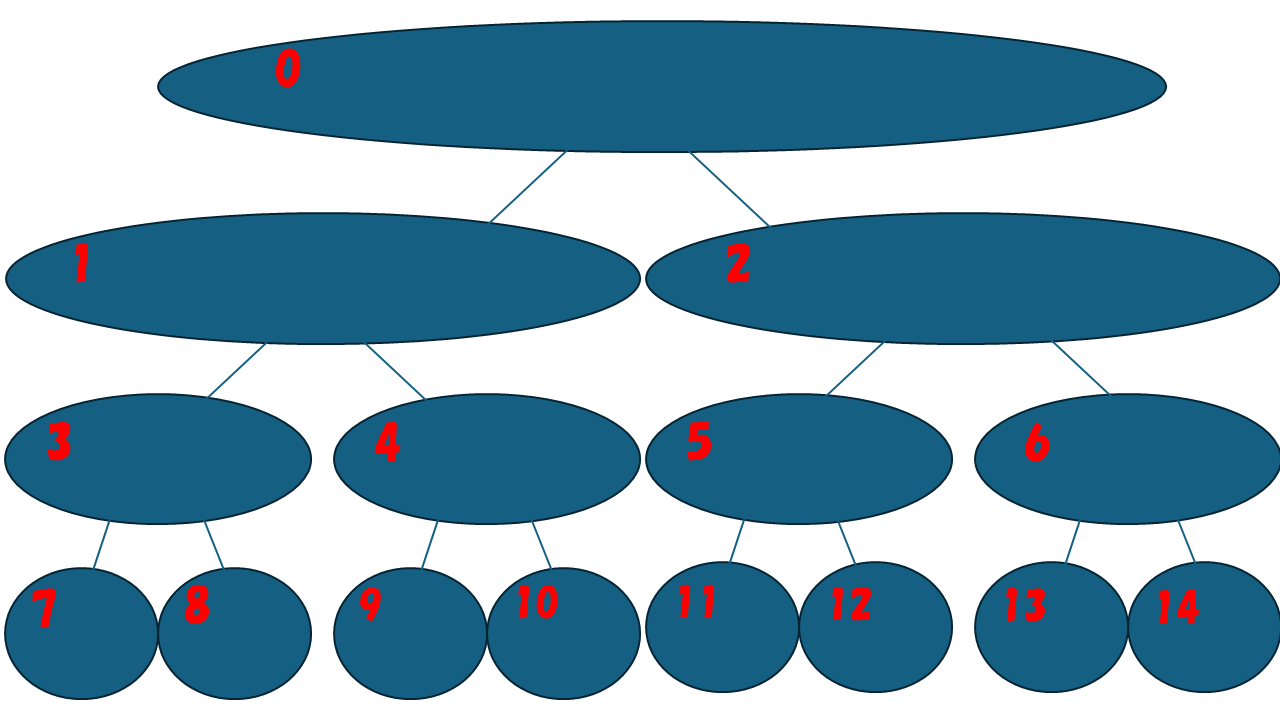



ここからは、データを載せていくことを考えます。

まず、葉に配列 A のデータを載せます。左の葉から順に、つまり、頂点 N - 1 から順に A の配列の要素を載せていきます。

ここで、葉が余ってしまいました。そのときにはダミーのデータを載せることを考えます。ダミーのデータとして、ダミーではないデータとの計算ではそのデータに影響を及ばさないようにしなければいけません。今回後に取り組む問題では、0 ≦ A_i ≦ 10 ^ 9 なので、任意の A_i において max(0, A_i) = A_i となりその他のデータには影響を及ぼさない事がわかります。そのため今回は 0 をダミーのデータとして使います。このようなものを単位元と言います。(詳細は問題 4)

ここまでのをまとめたのが下の木になります。黄色の数字がその頂点に載せたデータです。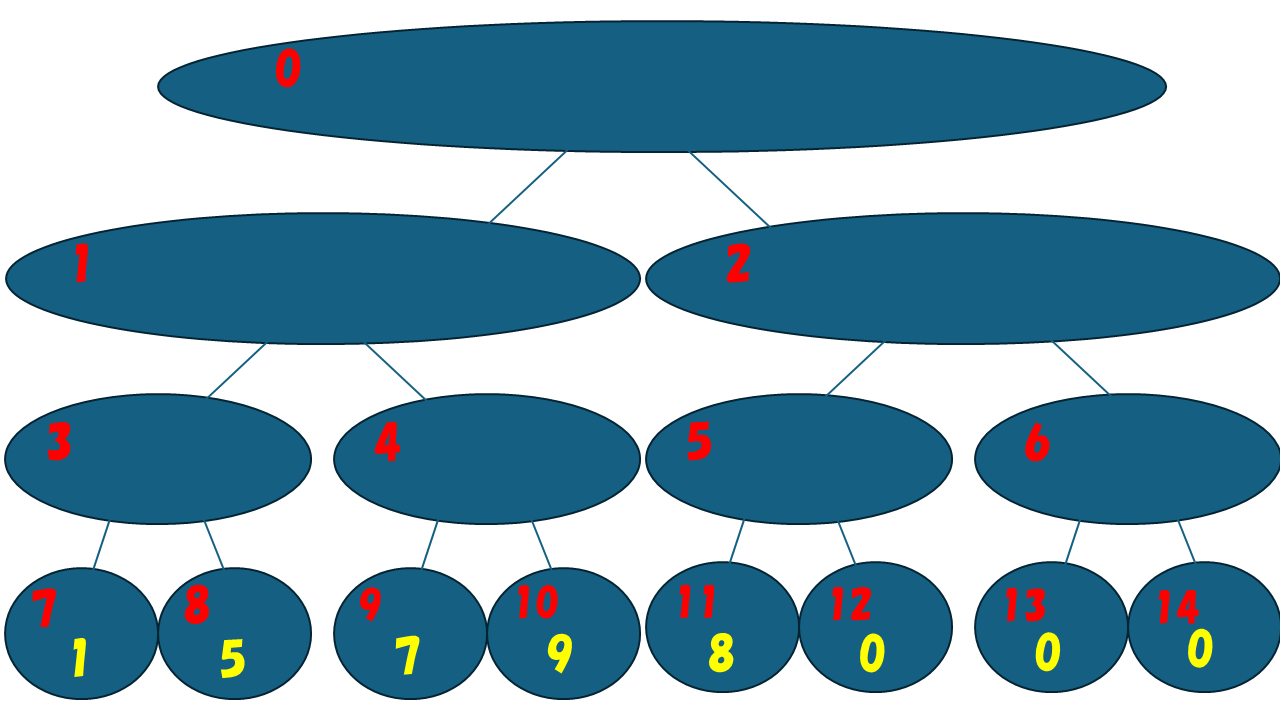



最後に葉以外の頂点にもデータを載せていきます。

葉以外の頂点については、2 つの子についてmax演算を行った結果を載せます。具体的には、頂点 i には、max((頂点番号 2 × i + 1 のデータ),(頂点番号 2 × i + 2 のデータ)) を載せます。このとき、計算順序としては、子の要素が確定していなければいけないので、葉に近い順、つまり、番号が大きいほうから計算していけばよいです。

ここまでのをまとめたのが下の木になり、これでSegment Treeの構築が終わりました。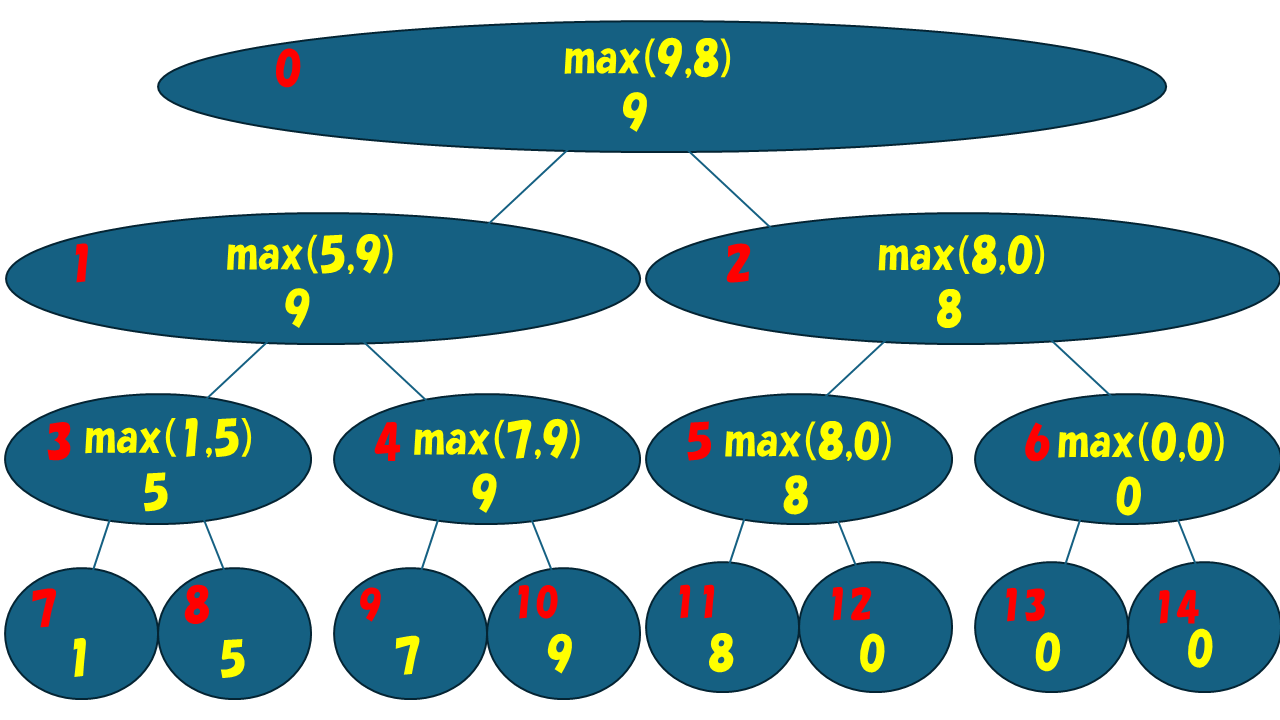



木の状態で管理するのは難しいため、実装では配列 (以降 Tree とする) で管理することとします。Tree の長さは完全二分木の頂点数とし、Tree の i 番目の要素は頂点 i に載せたデータを入れればよいです。この例では Tree = [9,9,8,5,9,8,0,1,5,7,9,8,0,0,0] となります。

では、以下の問題ではこの方法でSegment Treeを構築してみましょう。

(問題)

長さ n の配列 A が与えられます。上記の方法で求まる Tree を出力してください。ただし、ダミーのデータは 0 としてください。