(問題 1)Segment Treeの構築1 : 木について JavaScript編(paizaランク C 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
シェア用URL:
問題
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
(はじめに)
この問題集では、Segment Treeについて扱います。
Segment Treeでは区間クエリに加えて、1点更新も高速に行うことが出来るデータ構造です。
この問題集では、まず、構築、更新、区間クエリの処理の 3 つに分けて構成されています。
その後、Segment Treeを使う区間クエリの問題を解く流れになっています。
まずはじめに、Segment Treeを構築するために、グラフの知識について復習していきます。
以下にPythonコードの載せてあります。このコードを完成させることを目標とします。
class SegTree():
def calc(self, a, b): #区間クエリで行いたい処理
return max(a, b)
def e(self): #単位元
#問題 4 で説明
def __init__(self, n, A):
#完全2分木を構築
#問題 2,3 で実装
def renewal(self, ind, x): #A[ind]をxに更新
#問題 5,6 で実装
def product(self, l, r): #A[l]からA[r]までの計算結果を返す
#問題 7,8,9 で実装
まず、木について復習していきます。
木とは、連結成分が 1 つであり、閉路を持たないグラフのことです。
そのため、木の辺の数は (頂点の数)-1 本です。
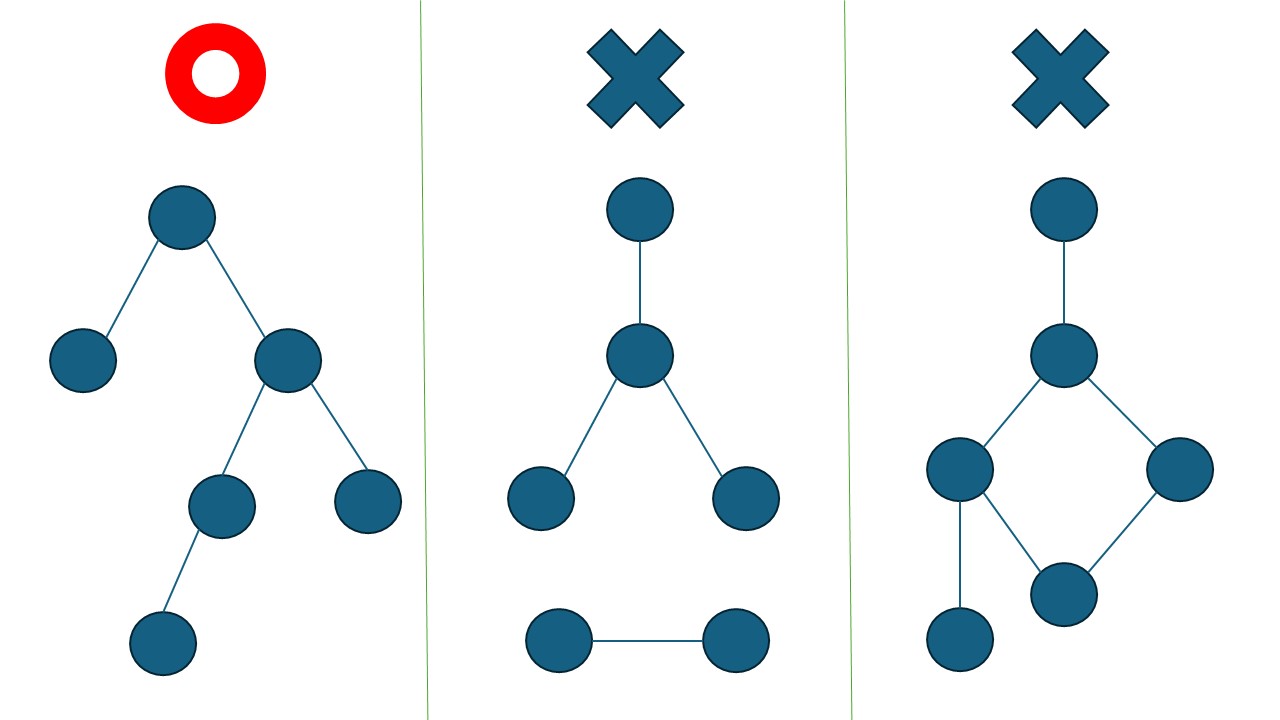
下の例でいうと、1 番左のグラフは連結成分が 1 であり、閉路を持っていないので木です。しかし、真ん中のグラフは連結成分が 2 であり、右のグラフは閉路を持っているため木ではありません。
木には、さまざまな管理方法があります。今回は隣接リストについてやっていきましょう。
隣接リストとはそれぞれの頂点に対し、隣接している頂点を管理したリストになります。では実際に管理してみましょう。
(問題)
N 頂点の木が与えられます。i (1 ≦ i ≦ N - 1) 番目の辺は頂点 a_i と頂点 b_i を結んでいます。
それぞれの頂点について隣接している頂点の番号を昇順に出力してください。
頂点番号が 0 始まりであることに注意してください。
- 入力される値
-
入力は以下のフォーマットで与えられます。
N
a_1 b_1
a_2 b_2
a_3 b_3
...
a_{N-1} b_{N-1}
1 行目には 1 つの整数 N が与えられます。
1 + i (1 ≦ i ≦ N - 1) 行目には 2 つの整数 a_i,b_i が与えられます。
入力は合計 N 行からなり、入力値最終行の末尾に改行を 1 つ含みます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
答えを N 行で出力してください。
i (1 ≦ i ≦ N) 行目では、頂点 i - 1 に隣接している頂点の番号を昇順に出力してください。
- 条件
-
すべてのテストケースについて以下の条件を満たします。
- 2 ≦ N ≦ 200000
- 0 ≦ a_i,b_i ≦ N - 1 (1 ≦ i ≦ N - 1)
- a_i ≠ b_i (1 ≦ i ≦ N - 1)
- i ≠ j なら (a_i, b_i) ≠ (a_j, b_j) かつ (a_i, b_i) ≠ (b_j, a_j)
- 与えられるグラフは木である
- 入力例1
-
6
1 2
1 3
3 4
4 5
3 0
- 出力例1
-
3
2 3
1
0 1 4
3 5
4
- 入力例2
-
2
0 1
- 出力例2
-
1
0

