最小の運賃
(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！
下記の問題をプログラミングしてみよう！
あなたは鉄道での旅行を計画しています。最寄り駅と目的の駅を含む合計 V 箇所の駅があり、どの駅を通過するかによって運賃が変わります。
あなたは旅費の節約のために運賃を最小にしようと考えています。駅と駅の間の運賃が与えられるので目的の駅までの最小運賃を求めてください。
ただし、あなたは常に 0 番目の駅から出発するものとします。
入力例 1 の場合、以下の図のように
0 番目の駅から出発し、4 番目の駅を通り、3 番目の駅に到着すると、800 (500 + 300) 円かかりますが、0 番目、1 番目、4 番目、3 番目の順で 3 番目の駅に向かった場合、700 (200 + 200 + 300) 円になるため、期待される出力は 700 になります。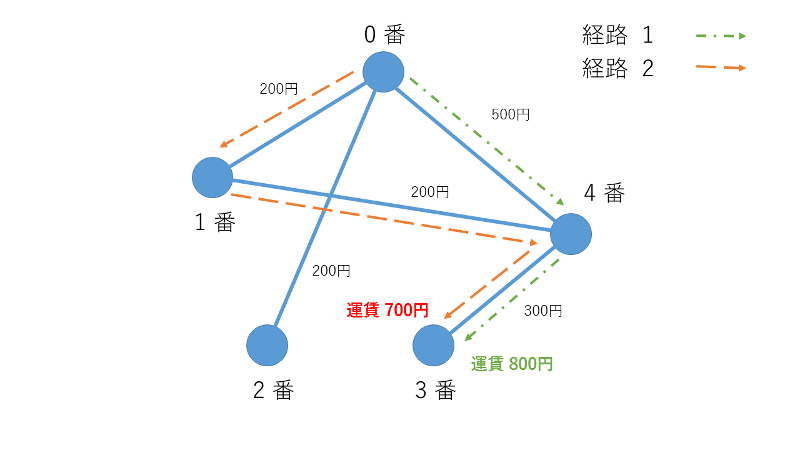
- 入力される値
-
入力は以下のフォーマットで与えられます。
E V T
s_1 e_1 c_1
s_2 e_2 c_2
...
s_E e_E c_E
・1 行目に路線の数 E、全ての駅の数 V、目的地の駅の番号 T が整数でこの順に半角スペース区切りで与えられます。
・続く E 行のうちの i 行目 (1 ≦ i ≦ E) には、s_i 番目の駅と e_i 番目駅の間の運賃を表す、c_i がこの順で半角スペース区切りで与えられます。
・入力は合計で E + 1 行となり、入力値最終行の末尾に改行が １ つ入ります。
入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
0 番目の駅から出発し、T 番目の駅に到着する経路の最低運賃を整数で出力してください。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・1 ≦ E ≦ 5,000
・2 ≦ V ≦ 100
・0 ≦ T < V
・0 ≦ s_i, e_i < V (1 ≦ i ≦ N)
・s_i ≠ e_i
・i ≠ j (1 ≦ i, j ≦ N) ならば、(s_i, e_i) ≠ (s_j, e_j) かつ (s_i, e_i) ≠ (e_j, s_j)
・1 ≦ c_i ≦ 1,000 (1 ≦ i ≦ E)
・0 番目の駅から T 番目の駅への経路は必ず存在する。
- 入力例1
-
5 5 3
0 1 200
0 4 500
0 2 200
1 4 200
4 3 300
- 出力例1
-
700
- 入力例2
-
3 6 3
0 1 200
1 3 150
2 4 100
- 出力例2
-
350
