ベクトルの応用 1 JavaScript編（paizaランク B 相当）
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！
シェア用URL:
ツイートする
問題
下記の問題をプログラミングしてみよう！
N 次元ベクトル a = (a_1, a_2 , ..., a_N) と b = (b_1, b_2, ..., b_N) が与えられます。
ベクトル a, b はそれぞれ N 次元空間 (直線 (N=1)・平面 (N=2)・3 次元空間・...) 内にある点の座標を表しています。
ここで、点 a と点 b のユークリッド距離 D(a, b) は次のように定義されます。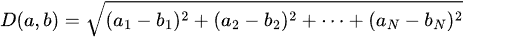
また、ユークリッド距離 D(a, b) を 2 乗した値 {D(a, b)}^2 は次のようになります。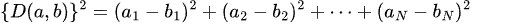
これまで説明したベクトルの引き算と内積を使うと、座標 a と b のユークリッド距離の 2乗 {D(a, b)}^2 は、
{D(a, b)}^2 = (a - b)・(a - b).
として計算することができます(・ は内積を表しています) 。
点 a, b のユークリッド距離の 2 乗 {D(a, b)}^2 を計算してください。
- 入力される値
-
N
a_1 a_2 ... a_N
b_1 b_2 ... b_N
・1 行目ではベクトルの要素数 N が与えられます。
・2 行目ではベクトル a が空白区切りで与えられます。
・3 行目ではベクトル b が空白区切りで与えられます。
入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
点 a と点 b のユークリッド距離の 2 乗 {D(a, b)}^2 を 1 行で出力してください。
末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて, 以下の条件をみたします
・入力はすべて整数
・1 ≦ N ≦ 100
・-10^3 ≦ a_i, b_i ≦ 10^3 (1 ≦ i ≦ N)
- 入力例1
-
2
0 0
1 2
- 出力例1
-
5
- 入力例2
-
5
1 2 3 4 5
1 2 3 4 5
- 出力例2
-
0
- 入力例3
-
3
1 2 3
2 -2 10
- 出力例3
-
66
