回転行列 Java編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
回転行列と呼ばれる行列を用いることで、XY平面上の点を、原点を軸にして半時計回りに M 度回転させることができます。
例えば M =0, 90, 180, 270 のとき、その回転行列 R_M はそれぞれ次のようになります。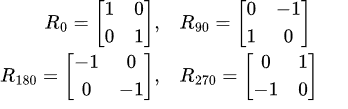
平面上のある点の座標を、 p_{1,1} が X 座標、p_{2,1} が Y 座標 であるような行列 (または列ベクトル) P で表します。
すると、M 度回転した後の点の座標は、q_{1,1} が X 座標、q_{2,1} が Y 座標 であるような行列 (または列ベクトル)を Q とすると、Q = R_M ✕ P として求めることができます。
回転の角度 M (M = 0, 90, 180, 270) と、平面上のある点の座標を表す 2 行 1 列のベクトル(列ベクトル) P が与えられます。
点 P を原点を軸にして半時計回りに M 度回転させたときの座標 Q を求めてください。
例えば、入力例 1 は座標 P = (1, 0) にある点を M=90 度回転させる入力が与えられます。
このとき、回転後の点の座標は Q=(0, 1) となります。 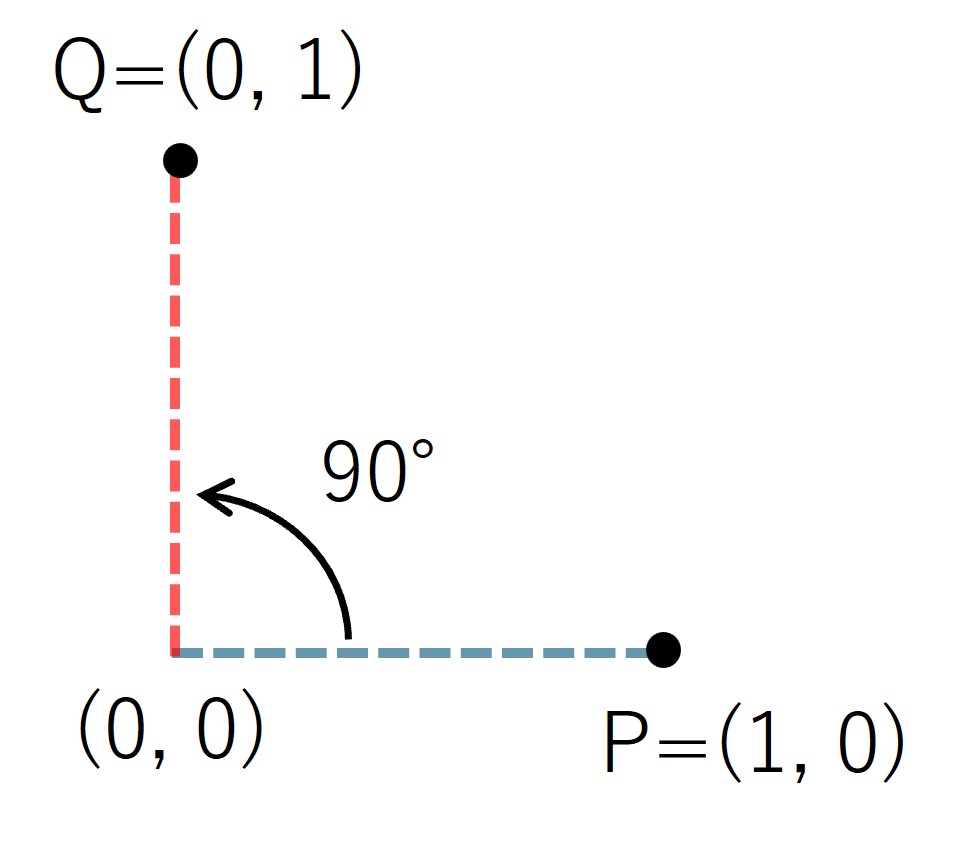
入力例 2 は座標 P = (2, 3) にある点を M=180 度回転させる入力が与えられます。
このとき、回転後の点の座標は Q=(-2, -3) となります。 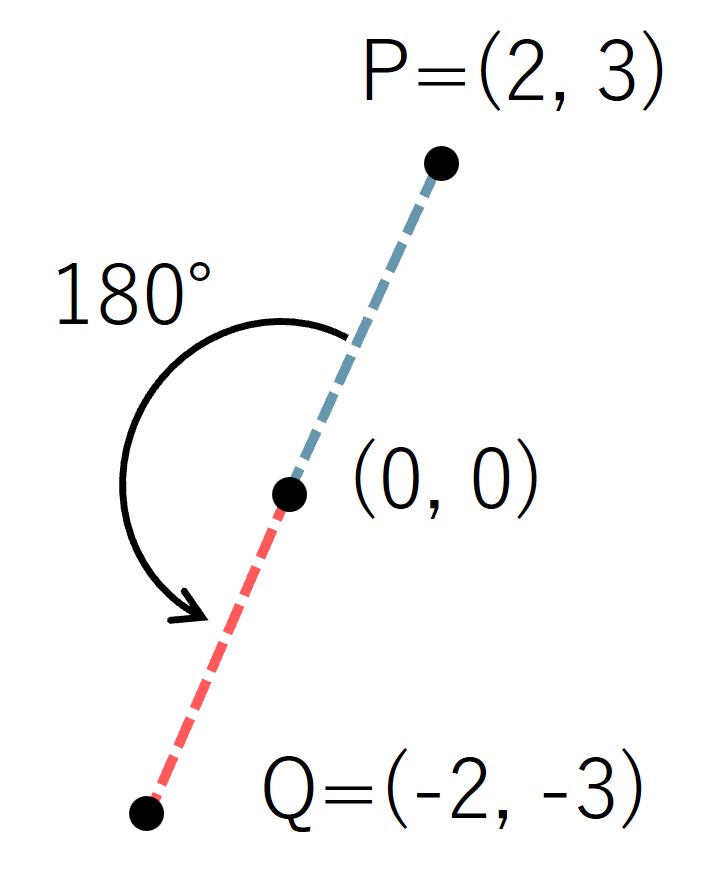
入力例 3 は座標 P = (3, 3) にある点を M=270 度回転させる入力が与えられます。
このとき、回転後の点の座標は Q=(3, -3) となります。 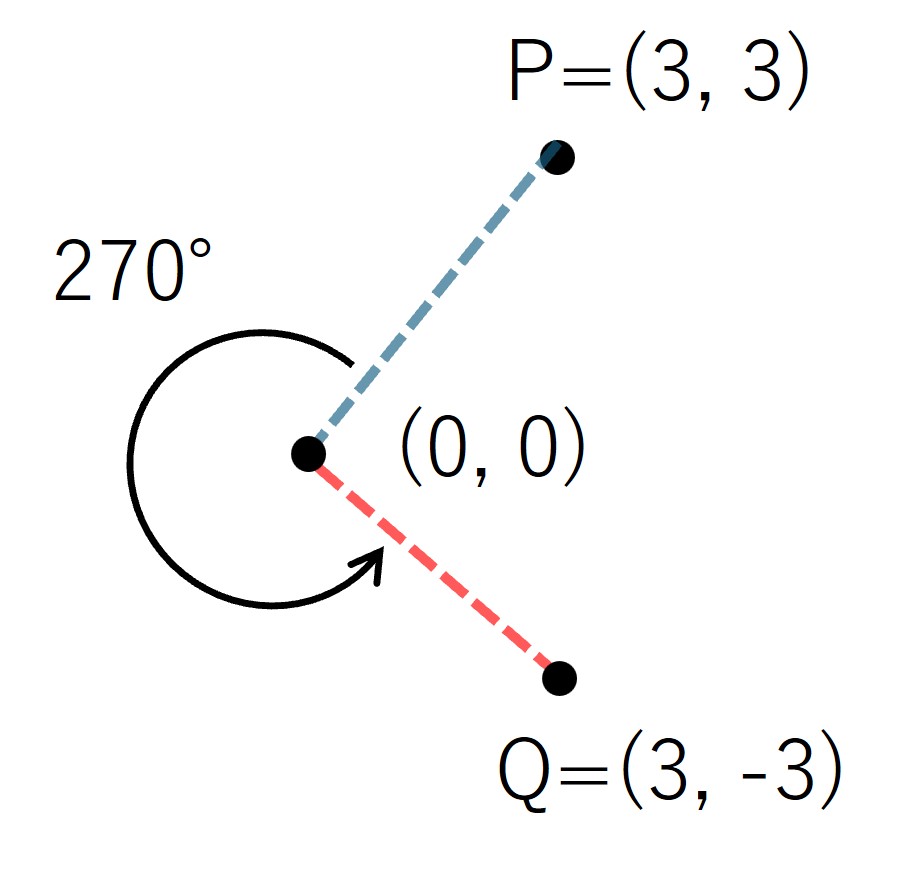
- 入力される値
-
M
p_{1,1}
p_{2,1}
・1 行目では回転の角度 M が与えられます。
・2 行目では点の X 座標 p_{1,1} が与えられます。
・3 行目では点の Y 座標 p_{2,1} が与えられます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
回転後の点の座標 Q を次のフォーマットにしたがって出力してください。
このとき、q_{1,1} は回転後の点の X 座標、q_{2,1} は回転後の点の Y 座標を表します。q_{1,1}
q_{2,1}
末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて, 以下の条件をみたします
・入力はすべて整数
・-10^3 ≦ p_{1,1}, p_{2,1} ≦ 10^3
- 入力例1
-
90
1
0
- 出力例1
-
0
1
- 入力例2
-
180
2
3
- 出力例2
-
-2
-3
- 入力例3
-
270
3
3
- 出力例3
-
3
-3

