ハミング符号 3 Java編（paizaランク A 相当）

ハミング符号の手順はおおまかに次の 3 つに分かれます。
(1) データを符号化する
(2) 誤りがあるかを判定する
(3) 誤り訂正をおこなう

この問題は、(3) の「誤り訂正をおこなう」という手順に対応します。

0, 1 のみを要素に持つ行列 (行ベクトル) w = [w_1 w_2 ... w_7] が与えられます。
まず、次の行列 H を用いて、行列 (行ベクトル) r = w✕H を計算してください。
この計算によって得られた r は 3 つの要素からなるベクトルです。
必要に応じて、後述する配列・リストを利用しても構いません。
(問題文はまだ続きます。)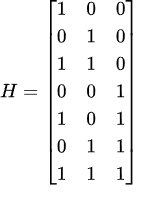

// 行列 H, C++用
{{1, 0, 0},
 {0, 1, 0},
 {1, 1, 0},
 {0, 0, 1},
 {1, 0, 1},
 {0, 1, 1},
 {1, 1, 1}}

# 行列 H, Python 用
[[1, 0, 0],
 [0, 1, 0],
 [1, 1, 0],
 [0, 0, 1],
 [1, 0, 1],
 [0, 1, 1],
 [1, 1, 1]]

次に、i 番目の要素 s_i を r の各要素 r_i (1 ≦ i ≦ 3) を 2 で割った余りとする行列 (行ベクトル) s = [s_1 s_2 s_3] = [r_1%2 r_2%2 r_3%2] を求めてください。
このとき、s = [0, 0, 0] である(s のすべての要素が 0 である)なら、行ベクトル w を出力して終了してください。

s ≠ [0, 0, 0] である場合はさらに次の手順を行ってください。
「j 番目の要素だけが 1 で、他の要素が 0 である 7 次元行ベクトル」をe_j (1 ≦ j ≦ 7) とします。
例えば e_1 = [1, 0, 0, 0, 0, 0, 0], e_4 = [0, 0, 0, 1, 0, 0, 0] です。
ここで、 p = e_j ✕ H とし、k 番目の要素 q_k を p の各要素 p_k (1 ≦ k ≦ 3) を 2 で割った余りとする行列 (行ベクトル)を q = [q_1 q_2 q_3] = [p_1%2 p_2%2 p_3%2] とします。
このとき、q = s が成り立つような整数値 j が 1 つ存在します(そのような j が存在する w が入力として与えられます)。
まず、そのような j を求めてください。

その後、行ベクトル x = w + e_j とし、さらに k 番目の要素 y_k を x の各要素 x_k (1 ≦ k ≦ 7) を 2 で割った余りとする行ベクトル y = [y_1 y_2 .. y_7] = [x_1%2 x_2%2 ... x_7%2]を出力してください。