隣接行列 4 Go編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
グラフにおいて、頂点 i から L 本の辺を経由して頂点 j にいく経路を「 i から j への長さ L の経路」と呼びます。
このような経路はグラフアルゴリズム (例えば幅優先探索) で求めることができますが、グラフが隣接行列で表されているときには行列計算によって求めることができます。
A の n 乗 A^n は A を n 回かけた行列です。
例えば A^1 = A, A^2 = A✕A, A^3 = A✕A✕A です。
隣接行列 A があるとき、A を n 乗した行列の i 行 j 列目の要素 は頂点 i から頂点 j への長さ n の経路の本数を表しています。
例えば、A^2 の i 行 j 列目の要素 は頂点 i から頂点 j への長さ 2 の経路の本数を表しています。
隣接行列 A の i 行 j 列目の要素 a_{i, j} は頂点 i と頂点 j をつなぐ辺の本数だったことを思い出してください。
行列 A と A の掛け算から得られる行列 A^2 の i 行 j 列目の 要素 c_{i,j} は A の i 行目の行ベクトルと A の j 列目の列ベクトルの内積となります。 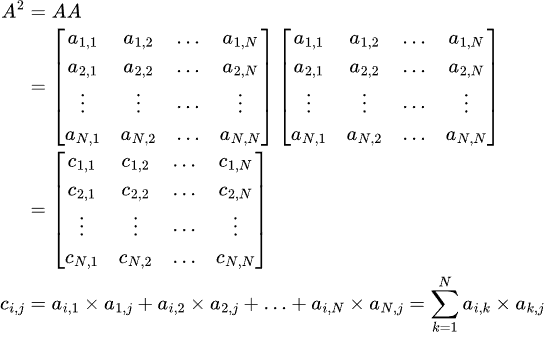
このとき、頂点 i からある頂点 k (1 ≦ k ≦ N) のみを経由して頂点 j に行く長さ 2 の経路の本数は、
a_{i, k} ✕ a_{k, j} として求めることができます。
したがって、頂点 i から頂点 j への長さ 2 の経路の本数は
a_{i, 1} ✕ a_{1, j} + a_{i, 2} ✕ a_{2, j} + ... + a_{i, N} ✕ a_{k, N}
として求めることができます。
これは A の i 行目の行ベクトルと A の j 列目の列ベクトルの内積です。
したがって、A^2 の i 行 j 列目の要素 c_{i, j} は頂点 i から頂点 j への長さ 2 の経路の本数となります。
無向グラフ(辺に向きがないグラフ)の隣接行列である N 次正方行列 A と頂点番号 X が与えられます。
頂点 1 から頂点 X への長さ L の経路の数を 1000 で割った余りを求めてください。
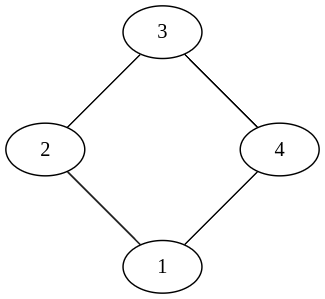
例えば、入力例 1 の隣接行列が表すのは次のようなグラフです。
このとき、頂点 1 から頂点 X=3 への長さ L=2 の経路は次の 2 つです。
(1) 1 → 2 → 3
(2) 1 → 4 → 3
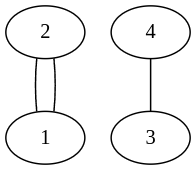
入力例 2 の隣接行列が表すのは次のようなグラフです。
このとき、頂点 1 から頂点 X=1 への長さ L=10 の経路は 1024 個あります。
したがって,1000 で割った余りである 24 が答えとなります。
入力例 3 の隣接行列が表すのは次のようなグラフです。
このとき、頂点 1 から頂点 X=5 への長さ L=100 の経路は 0 個あります。

- 入力される値
-
N X L
a_{1,1} a_{1,2} ... a_{1,N}
a_{2,1} a_{2,2} ... a_{2,N}
...
a_{N,1} a_{N,2} ... a_{N,N}
・1 行目では行列のサイズ N, 経路の終点 X, 経路の長さ L が与えられます。
・次の N 行では行列 A の要素 a_{i, j} が、行ごとに、空白区切りで与えられます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
与えられたグラフにおいて、頂点 1 から頂点 X への経路の数を 1000 で割った余りを 1 行で出力してください。
末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて, 以下の条件をみたします
・入力はすべて整数
・与えられる隣接行列が表すグラフは自己ループを持たない
・与えられる隣接行列が表すグラフは多重辺を持つ場合がある
・1 ≦ X ≦ N ≦ 100
・1 ≦ L ≦ 100
・0 ≦ a_{i, j} ≦ 100 (1 ≦ i, j ≦ N)
- 入力例1
-
4 3 2
0 1 0 1
1 0 1 0
0 1 0 1
1 0 1 0
- 出力例1
-
2
- 入力例2
-
4 1 10
0 2 0 0
2 0 0 0
0 0 0 1
0 0 1 0
- 出力例2
-
24
- 入力例3
-
5 5 100
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
- 出力例3
-
0

