隣接行列 3 C++編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
頂点数 N のグラフ G と H が与えられます。
グラフ G, H はそれぞれが 1 から N までの整数で番号付けされた頂点の集合を持ちます。
このとき、次のような頂点の変換 f と f による辺の変換を考えます。
・グラフ G の頂点 i のそれぞれの番号 (1, 2, ..., N) を、(1, 2, ..., N) を並び替えた(そのままでも良い) 数列 P の i 番目の要素 p_i に変える変換 f
・グラフ G の「頂点 u と v をつなぐ辺」を「頂点 f(u) と f(v) をつなぐ辺」に変える変換
このような変換をグラフ G におこなって得られるグラフ F は (1, 2, ..., N) の並び替えの個数である N! 通り存在しますが、グラフ F と H が一致するような変換が存在する場合、G と H は同型であると言います。
グラフが同型であることは、頂点の番号付けを無視すれば G と H が同じ形状のグラフであることを意味しています。
N 個の頂点からなる無向グラフ G, H をそれぞれ表す隣接行列 A, B が与えられます。
グラフ G と H が同型であるかを判定し、同型なら Yes、同型でないならNoを出力してください。
例えば、入力例 1 が表すのは次のようなグラフです。2 つのグラフは同型です。 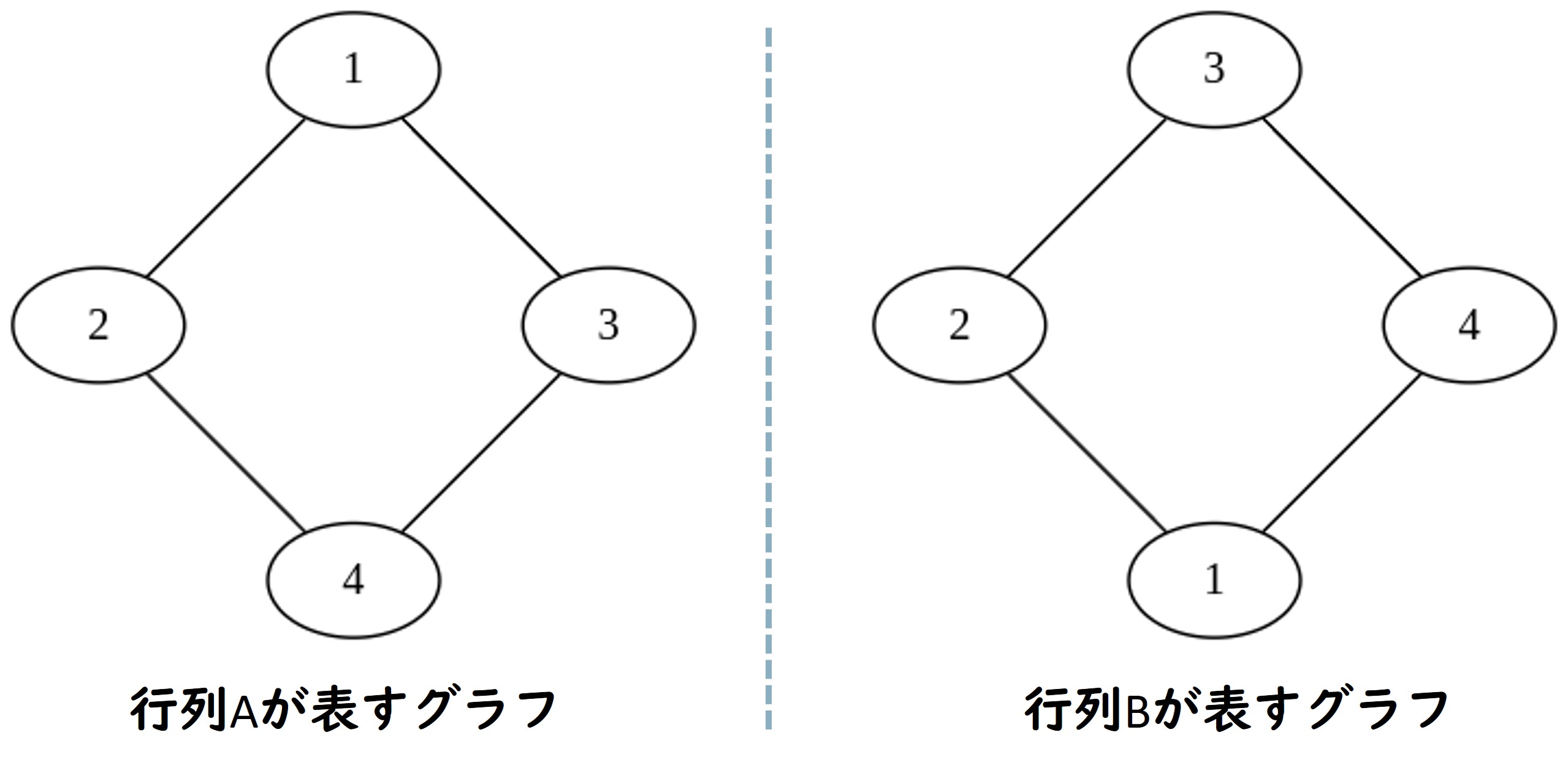
入力例 2 が表すのは次のようなグラフです。2 つのグラフは同型です。 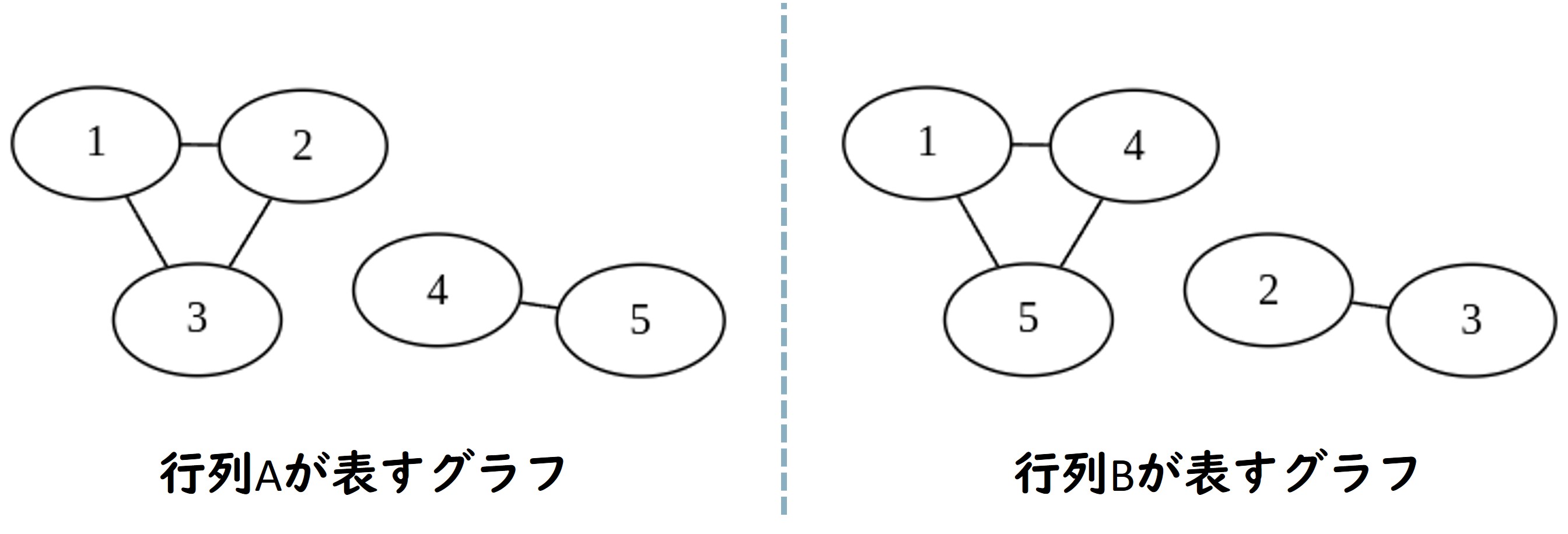
入力例 3 が表すのは次のようなグラフです。
2 つのグラフは頂点数は同じですが、辺数は異なります。このような場合、同型ではありません。 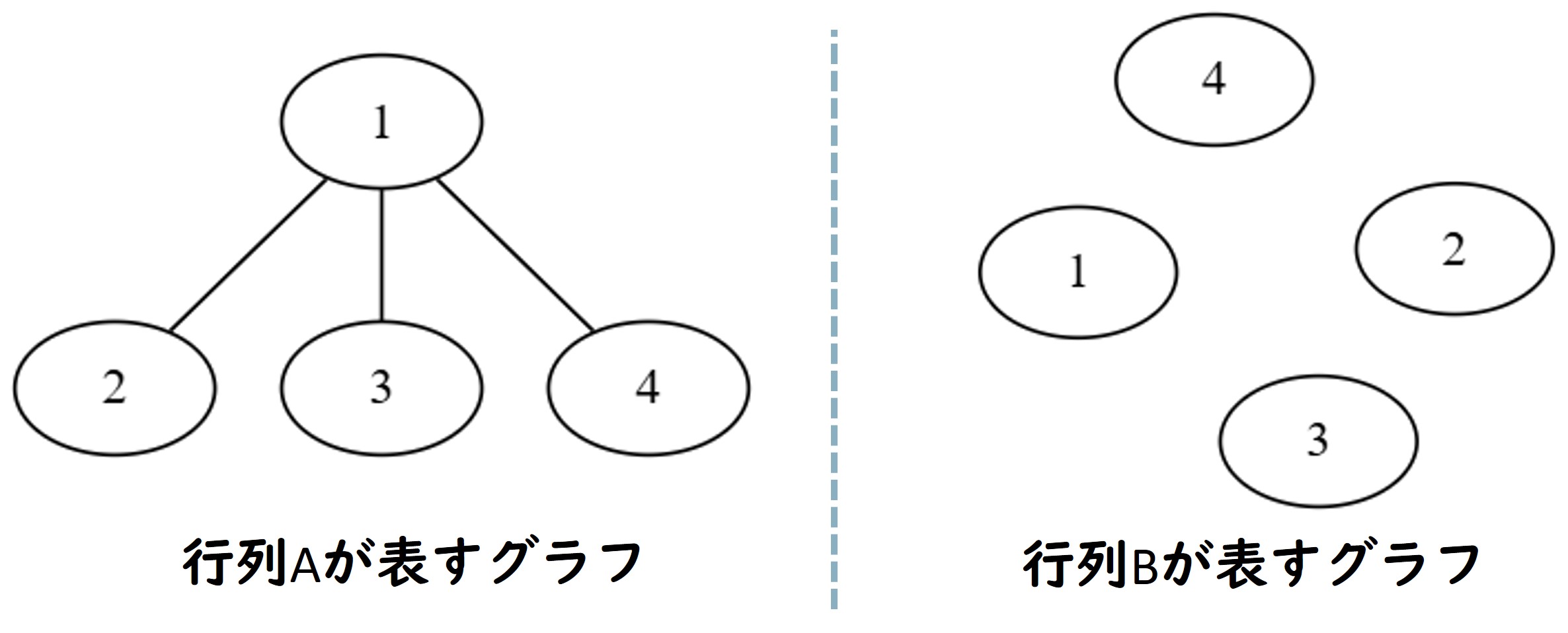
入力例 4 が表すのは次のようなグラフです。
2 つのグラフは頂点数と辺数は同じですが、同型ではありません。 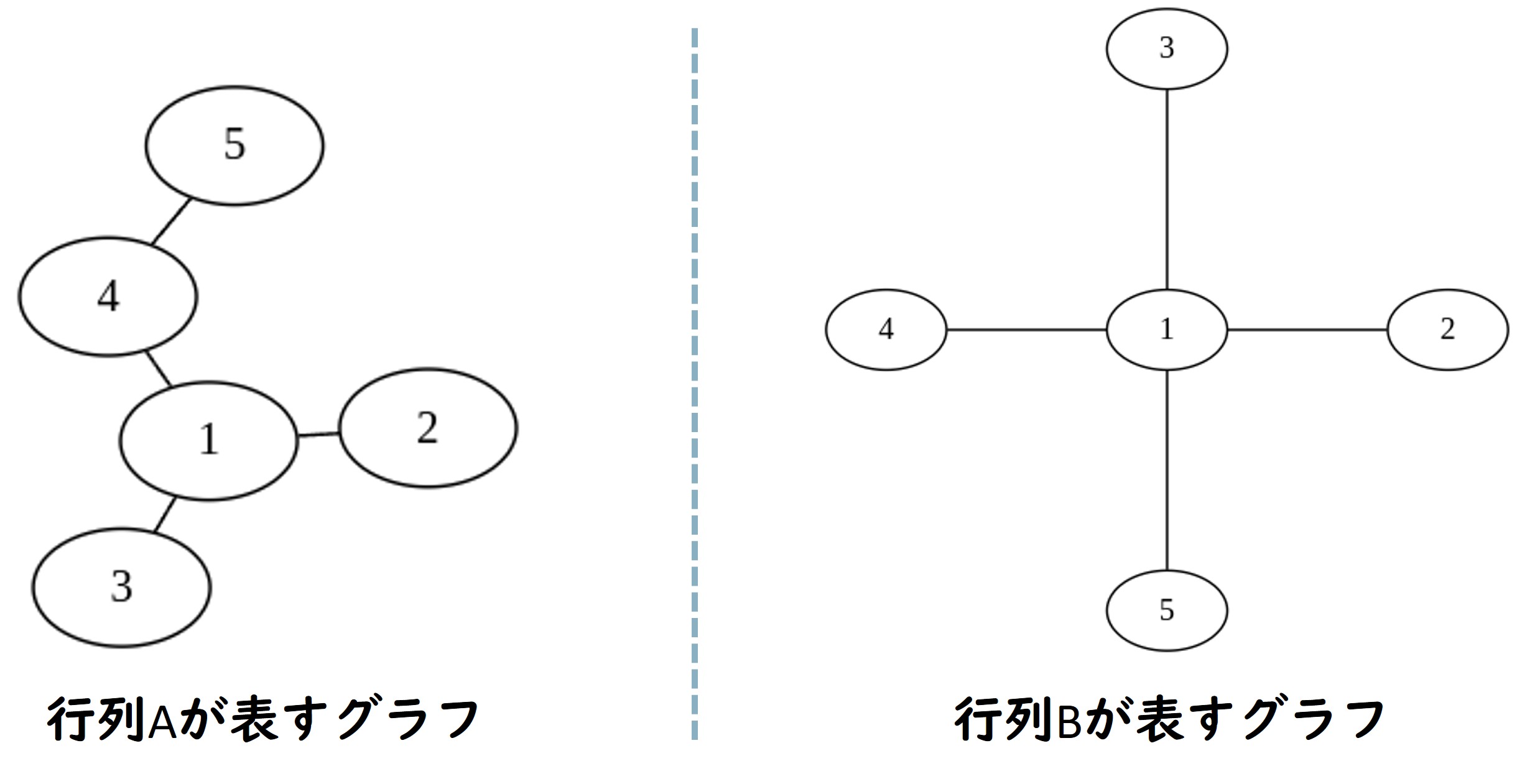
- 入力される値
-
N
a_{1,1} a_{1,2} ... a_{1,N}
a_{2,1} a_{2,2} ... a_{2,N}
...
a_{N,1} a_{N,2} ... a_{N,N}
b_{1,1} b_{1,2} ... b_{1,N}
b_{2,1} b_{2,2} ... b_{2,N}
...
b_{N,1} b_{N,2} ... b_{N,N}
・1 行目では行列のサイズ N が与えられます。
・次の N 行では行列 A の要素 a_{i, j} が、行ごとに、空白区切りで与えられます。
・次の N 行では行列 B の要素 b_{i, j} が、行ごとに、空白区切りで与えられます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
2 つのグラフが同型かを判定し、
YesまたはNoを出力してください。
末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて, 以下の条件をみたします
・入力はすべて整数
・与えられる隣接行列が表すグラフは自己ループを持たない
・与えられる隣接行列が表すグラフは多重辺を持たない
・1 ≦ N ≦ 8
・0 ≦ a_{i, j} ≦ 1 (1 ≦ i, j ≦ N)
- 入力例1
-
4
0 1 0 1
1 0 1 0
0 1 0 1
1 0 1 0
0 1 1 0
1 0 0 1
1 0 0 1
0 1 1 0
- 出力例1
-
Yes
- 入力例2
-
5
0 1 1 0 0
1 0 1 0 0
1 1 0 0 0
0 0 0 0 1
0 0 0 1 0
0 0 0 1 1
0 0 1 0 0
0 1 0 0 0
1 0 0 0 1
1 0 0 1 0
- 出力例2
-
Yes
- 入力例3
-
4
0 1 1 1
1 0 0 0
1 0 0 0
1 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
- 出力例3
-
No
- 入力例4
-
5
0 1 1 1 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 1
0 0 0 1 0
0 1 1 1 1
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0
1 0 0 0 0
- 出力例4
-
No

