シュトラッセンのアルゴリズム 2 Java編（paizaランク A 相当）

問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！

問題

下記の問題をプログラミングしてみよう！

1 つ前の問題では 2 ✕ 2 行列の計算を行いましたが、より大きいサイズの行列もブロック行列とみなすことで同様の手順で計算できます。
整数 N を 1 より大きい 2 のべき乗で表される数 (2, 4, 8, 16, 32, ...) とします。
ここで、N ✕ N 行列 A, B をそれぞれ次のような N/2 次正方行列 4 つからなるブロック行列とみなします。(図は行列 A に関してですが、行列 B も同じようにみなします。)

ここで、M_1, M_2, ..., M_7 を次のような行列として定義すると、行列 C = AB の各ブロック要素がこれらを用いて次のように計算できます。
これは 1 つ前の問題において求めた m_1, m_2, ..., m_7 を行列に変えたもので、ブロック行列の掛け算が通常の行列の掛け算 (内積を取る) と同様の式で表せることを利用しています。
行列積のこのような計算方法を「シュトラッセンのアルゴリズム」と呼びます。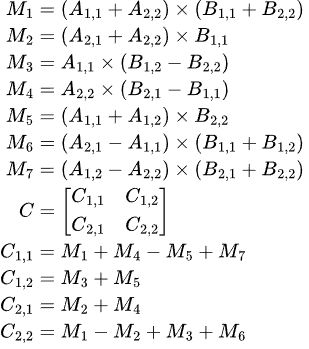

行列 A, B が与えられます。
行列 M_1, M_2, ..., M_7 を求め、これらの値を用いて、行列 A に B を掛けた結果となる行列 C を求めてください。

入力される値

N
a_{1,1} a_{1,2} ... a_{1,N}
a_{2,1} a_{2,2} ... a_{2,N}
...
a_{N,1} a_{N,2} ... a_{N,N}
b_{1,1} b_{1,2} ... b_{1,N}
b_{2,1} b_{2,2} ... b_{2,N}
...
b_{N,1} b_{N,2} ... b_{N,N}

・1 行目では行列のサイズ N が与えられます。
・次の N 行では行列 A の要素 a_{i, j} が、行ごとに、空白区切りで与えられます。
・次の N 行では行列 B の要素 b_{i, j} が、行ごとに空白区切りで与えられます。

入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。標準入力からの値取得方法はこちらをご確認ください

期待する出力

次のフォーマットに従い、行列 C = AB の i 行 j 列目の要素 c_{i, j} を、行ごとに、空白区切りで出力してください。

c_{1,1} c_{1,2} ... c_{1,N}
c_{2,1} c_{2,2} ... c_{2,N}
...
c_{N,1} c_{N,2} ... c_{N,N}

末尾に改行を入れ、余計な文字、空行を含んではいけません。

条件: すべてのテストケースにおいて, 以下の条件をみたします

・入力はすべて整数
・2 ≦ N ≦ 128
・整数 N は 1 より大きい 2 のべき乗で表される数が与えられる。つまり、N は 2, 4, 8, 16, 32, 64, 128 のいずれかの値となる。
・-10^3 ≦ a_{i, j}, b_{i, j} ≦ 10^3 (1 ≦ i ≦ N, 1 ≦ j ≦ N)

入力例1: 2
1 2
3 4
1 0
0 1

出力例1: 1 2
3 4

入力例2: 4
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16

出力例2: 1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16

入力例3: 8
5 3 2 1 -2 -2 1 4
3 0 1 2 1 -5 -3 -2
3 5 -4 5 -3 1 5 -4
-5 2 3 -3 -4 1 -1 5
2 -1 -5 -3 -4 2 0 2
5 -5 5 -4 0 4 -5 0
-4 -3 -4 -1 -4 2 -1 3
-3 0 0 -3 -1 -2 -4 2
-5 -2 1 -5 -2 4 3 5
-3 -2 -1 2 1 -2 -1 -3
-3 1 5 -3 0 -2 -5 4
2 -3 -3 2 -5 2 0 -4
3 -5 1 -1 5 0 -5 -1
-5 0 -5 1 -2 -4 3 -3
4 5 0 4 0 -3 2 1
-3 -4 -2 0 -2 3 4 -4

出力例3: -42 -18 9 -19 -26 29 24 13
8 -23 32 -32 3 37 -30 30
10 21 -37 41 -35 -11 36 -15
-32 13 -2 15 -5 -22 9 -27
-26 14 -31 3 -18 12 66 -5
-73 -8 27 -74 -3 11 -3 59
4 16 -38 26 -20 0 47 -38
-6 -8 11 -8 16 8 -10 -8

問題一覧へ戻る