ブロック行列の掛け算 C++編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
i 行 j 列目の要素が行列である行列をブロック行列 (または区分行列) と呼びます。
ブロック行列は通常の行列の要素をブロック分けしたもので、表現が異なるだけであり、通常の行列と違いはありません。
ブロック行列 A と B の掛け算は次のように定義されます。
ただし、この問題では A, B は N 次正方ブロック行列で、各要素 A_{i,j}, B_{i,j} (1 ≦ i,j ≦ N) は M 次正方行列とします。
実際には、ブロック行列の要素である行列 A_{i, j}, B_{i, j} は全て同じサイズの行列である必要はありません。
ブロック行列 A, B が与えられます。
A と B を掛けた結果となるブロック行列 C を計算してください。
入力例 1 において与えられるブロック行列 A, B およびブロック行列 C = AB は次のようになります。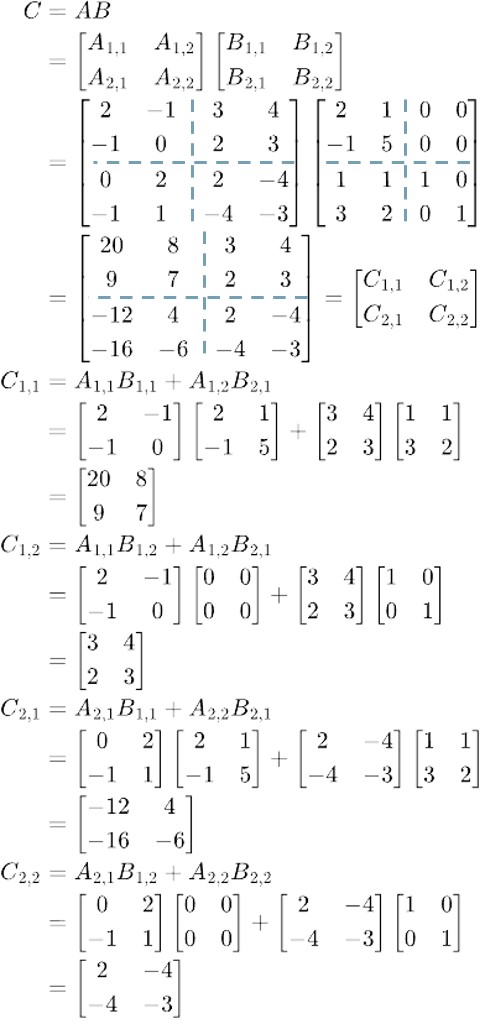
入力例 2 において与えられるブロック行列 A, B およびブロック行列 C = AB は次のようになります。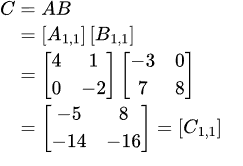
入力例 3 において与えられるブロック行列 A, B およびブロック行列 C = AB は次のようになります。
- 入力される値
-
N M
A_{1,1}
A_{1,2}
...
A_{1,N}
A_{2,1}
A_{2,2}
...
A_{2,N}
...
A_{N,N}
B_{1,1}
B_{1,2}
...
B_{1,N}
B_{2,1}
B_{2,2}
...
B_{2,N}
...
B_{N,N}
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
ブロック行列 C = AB の i 行 j 列目の要素となる行列 C_{i, j} を次のように出力してください。
ただし、C_{i, j} は後述するフォーマットにしたがって出力をおこなってください。C_{1,1}
C_{1,2}
...
C_{1,N}
C_{2,1}
C_{2,2}
...
C_{2,N}
...
C_{N,N}
行列 C_{i, j} は M 次正方行列です。その h 行 w 列目の要素を c_{h, w} と表記します。
行列 C_{i, j} はそれぞれ次のフォーマットに従い、行ごとに、空白区切りで出力をおこなってください。c_{1,1} c_{1,2} ... c_{1,M}
c_{2,1} c_{2,2} ... c_{2,M}
...
c_{M,1} c_{M,2} ... c_{M,M}
末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて, 以下の条件をみたします
・入力はすべて整数
・1 ≦ N, M ≦ 10
・-10^3 ≦ a_{h, w}, b_{h, w} ≦ 10^3 (1 ≦ h ≦ M, 1 ≦ w ≦ M)
- 入力例1
-
2 2
2 -1
-1 0
3 4
2 3
0 2
-1 1
2 -4
-4 -3
2 1
-1 5
0 0
0 0
1 1
3 2
1 0
0 1
- 出力例1
-
20 8
9 7
3 4
2 3
-12 4
-16 -6
2 -4
-4 -3
- 入力例2
-
1 2
4 1
0 -2
-3 0
7 8
- 出力例2
-
-5 8
-14 -16
- 入力例3
-
3 1
2
6
-2
0
-1
3
3
0
6
6
4
-3
3
1
-1
-5
-2
2
- 出力例3
-
40
18
-16
-18
-7
7
-12
0
3

