準オイラーグラフ・無向グラフ(paizaランク B 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
いくつかの頂点と、それらのうち 2 つの頂点を結ぶ辺の集合をグラフといいます。特に、辺に向きがつけられていない場合は無向グラフといいます。
さらに、どの 2 つの頂点間も辺をたどって行き来ができるような場合は、連結なグラフといいます。下の図は、頂点の数が 5 の連結な無向グラフの一例です。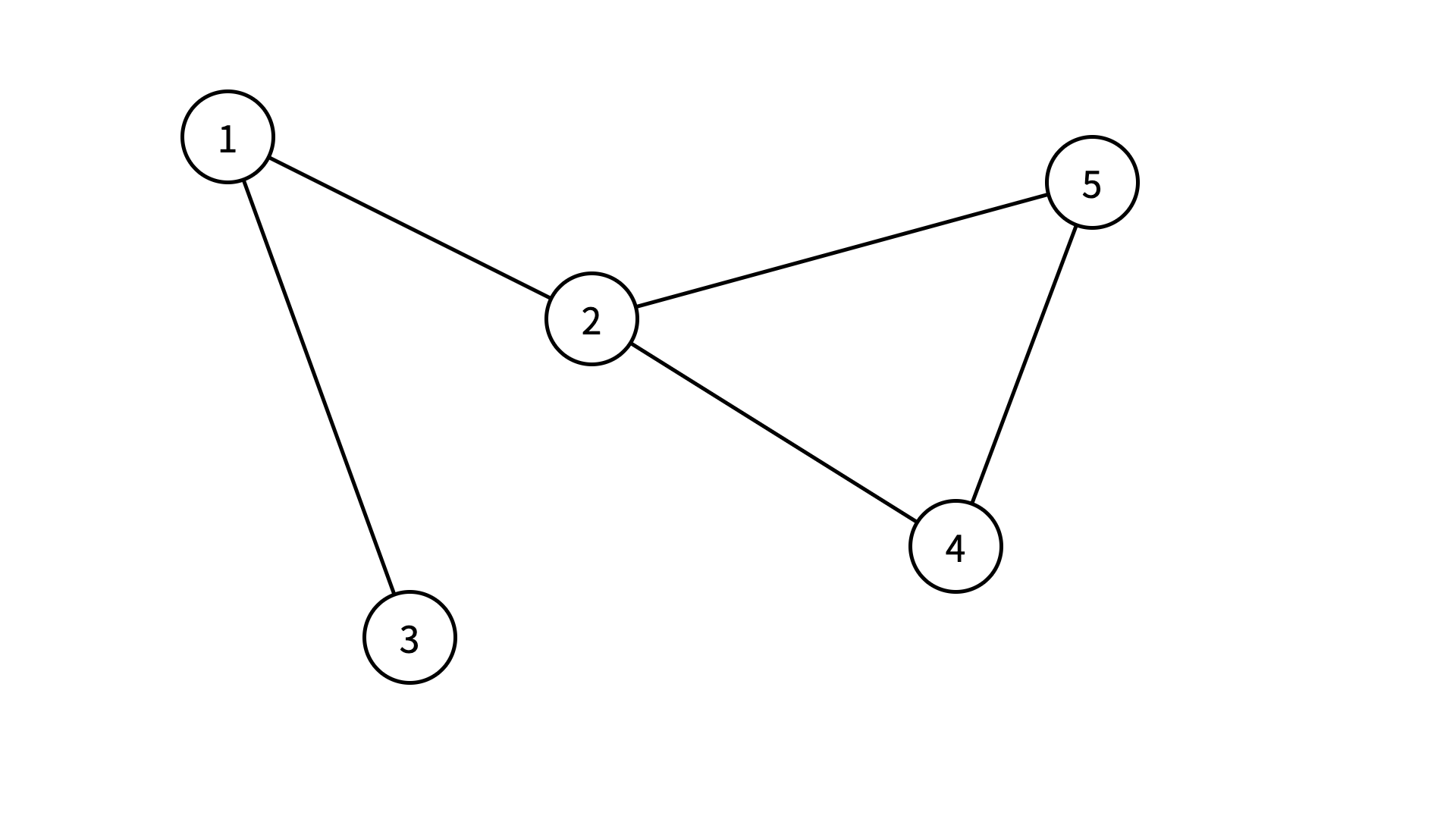
1, ..., n の番号がついた n 個の頂点と、1, ..., m の番号がついた m 個の辺からなる連結な無向グラフを考えます。
整数 n, m と、m 個の頂点の組 (a_1, b_1), ..., (a_m, b_m) が与えられます。
頂点の組 (a_i, b_i) は、頂点 a_i と 頂点 b_i が辺で直接つながっていることを表します。
(頂点 a_i と 頂点 b_i が辺で直接つながっているとき、頂点 b_i と 頂点 a_i も辺で直接つながっているといえます。)
そして、これら以外に辺で直接つながっている頂点の組はありません。
このとき、以下の条件を用いて、このグラフにおいて、すべての辺を一筆書きすることができるかどうか判定してください。ただし、この問題では最終的に初めの頂点に戻らなくても良いものとします。なお、そのようなことが可能なグラフを準オイラーグラフといいます。
連結な無向グラフにおいて、すべての辺を一筆書きすることができるための必要十分条件は以下のようになります。
・次数が奇数である頂点の個数が、ちょうど 0 または 2 である。
ただし、ここでいう次数とは、以下の形式で表現されるものとします。
頂点 i をつないでいる辺の個数を頂点 i の次数といいます。
ただし、辺がループの場合は、その辺に対して 2 回分数えるものします。
下の図は、ある無向グラフの頂点の次数を表したものです。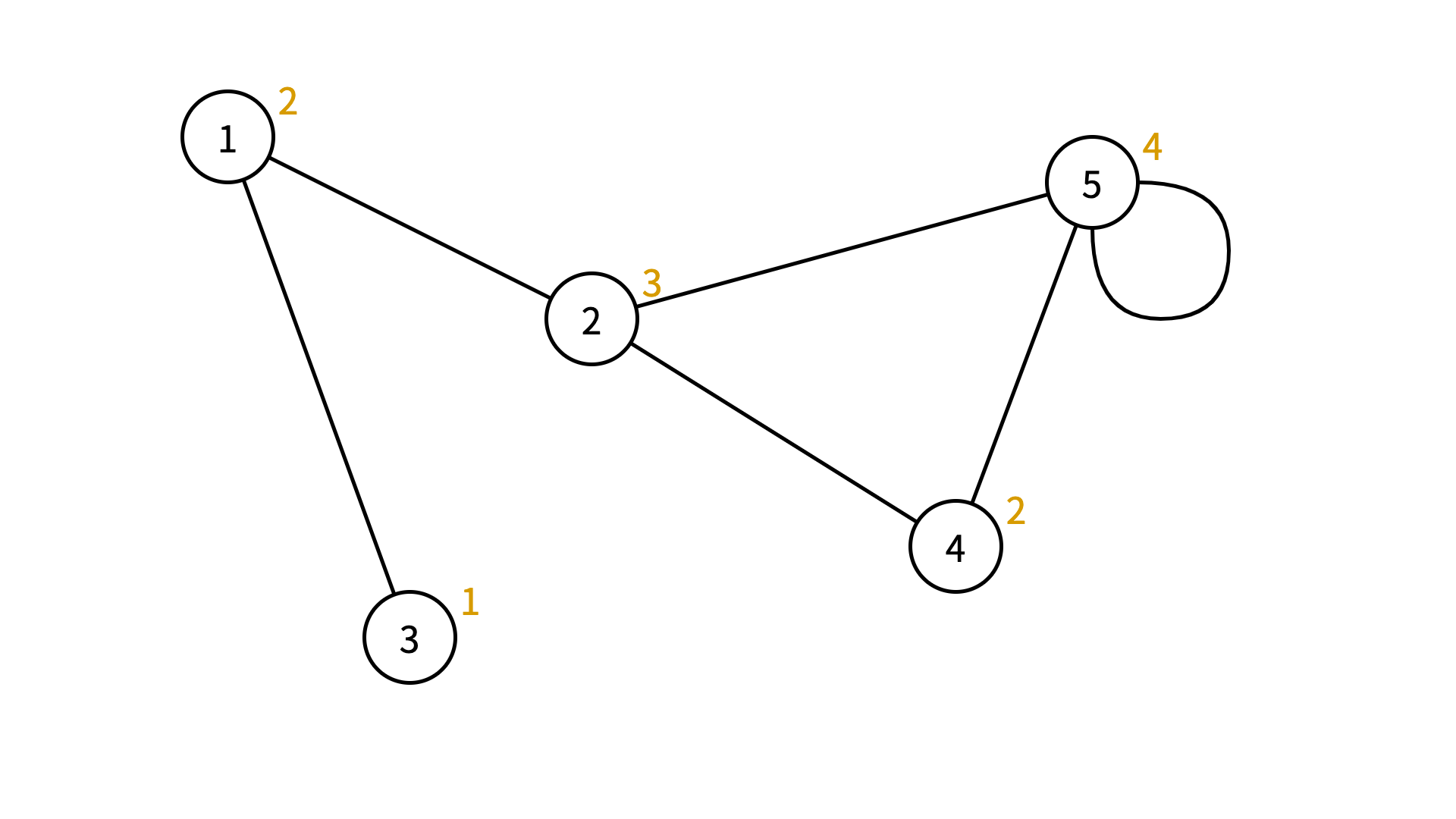
- 入力される値
-
n m
a_1 b_1
...
a_m b_m
・ 1 行目に、頂点の個数を表す整数 n と、頂点の組の個数を表す整数 m が半角スペース区切りで与えられます。
・ 続く m 行では、頂点の組 a_i, b_i が半角スペース区切りで与えられます。(1 ≦ i ≦ m)
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
与えられたグラフにおいて、すべての辺を一筆書きすることができる場合は 1, そうでない場合は 0 を出力してください。
また、末尾に改行を入れ、余計な文字を含んではいけません。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・ 入力はすべて整数
・ 2 ≦ n ≦ 100
・ n - 1 ≦ m ≦ 10000 = 10^4
・ 1 ≦ a_i ≦ b_i ≦ n
・ 与えられるグラフは連結である
- 入力例1
-
3 2
1 2
2 3
- 出力例1
-
1
- 入力例2
-
3 4
1 2
1 2
2 3
2 3
- 出力例2
-
1
- 入力例3
-
4 3
1 2
1 3
1 4
- 出力例3
-
0

