(問題 3) イチゴ争奪戦 step.3 JavaScript編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
N 個のセグメントに分かれている 1 次元のケーキがあり、i (1 ≦ i ≦ N) 番目のセグメントには A_i 個のイチゴが載っています。
k = 0, 1, ..., N - 2 に対して、それぞれ以下の問題の答えを求めてください。
左から k 個のセグメント分のケーキを食べてしまいました。残ったセグメントの中から切れ目を 1 つ選び、2 つのケーキに分けます。2 つのケーキに乗っているイチゴの数の差の最小値を求めてください。
(制約) 2 ≦ N ≦ 200000, 1 ≦ A_i ≦ 10 ^ 9 (1 ≦ i ≦ N)
この問題を解いてみましょう。問題 1, 2 と同じように全ての k に対して切れ目を全部試してみては、O(N ^ 2) になってしまい間に合いません。
そこで今回は、答えになる切れ目の性質をもとにさらに高速に答えを求めることを考えましょう。
問題 1 で見てきた例をまた見ていきます。
7 個のセグメントに左からイチゴが、8 個、12 個、13 個、7 個、2 個、17 個、6 個載っている状況を考えます。今回は、説明を簡単にするため、本来は切れ目でない 1 番左のセグメントの左端と、 1 番右のセグメントの右端も切れ目として扱います。
2 番目のセグメントと 3 番目のセグメントの間で切れ目を入れています。左のケーキは 20 個のイチゴが、右のケーキには 45 個のイチゴが載っていることがわかります。つまり、この状況では右のケーキのほうが多くイチゴが載っています。このような切れ目を右得切れ目とします。
同様に 5 番目のセグメントと 6 番目のセグメントの間で切れ目を入れています。左のケーキは 42 個のイチゴが、右のケーキには 23 個のイチゴが載っていることがわかります。つまり、この状況では左のケーキのほうが多くイチゴが載っています。このような切れ目を左得切れ目とします。(左右同数の場合も左得切れ目とします。)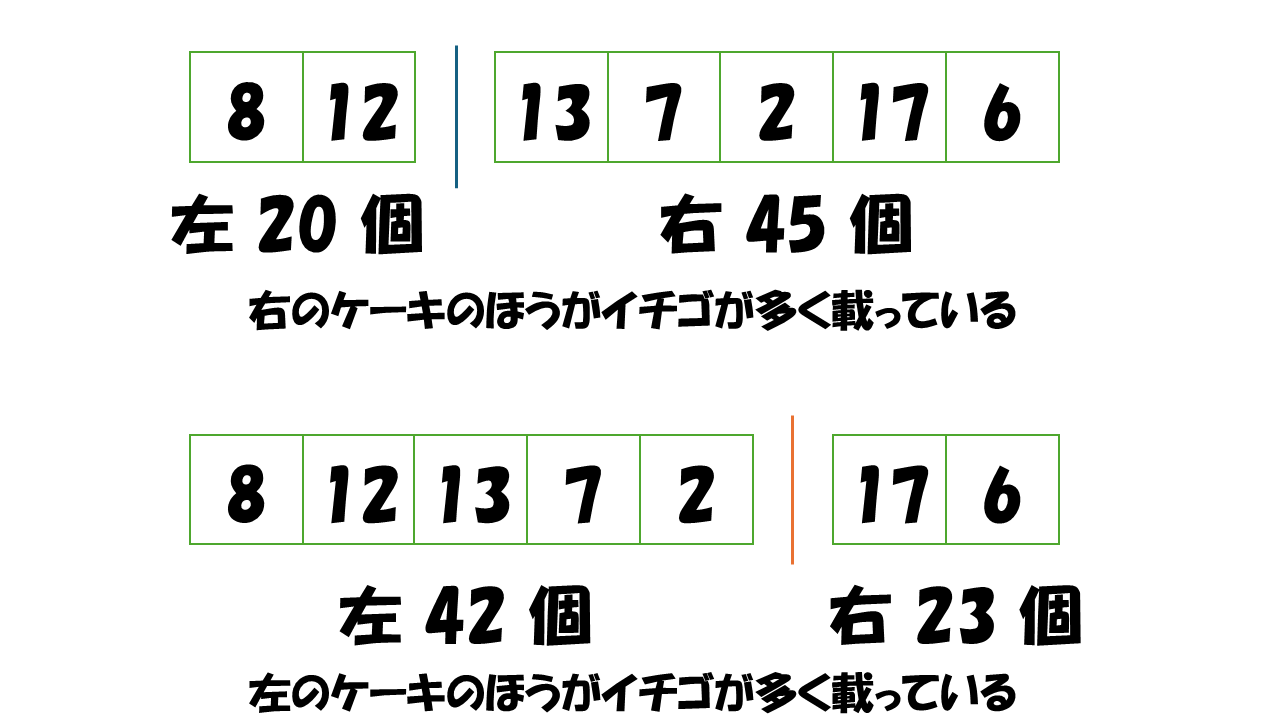
それぞれの切れ目で先ほどと同じように左の切れ目から見てみると、左のケーキのイチゴの数は右に切れ目を移すたび増え、右のケーキのイチゴの数は右に切れ目を移すたびに減るので、右得切れ目から、左得切れ目にちょうど 1 回だけ移り変わることがわかります。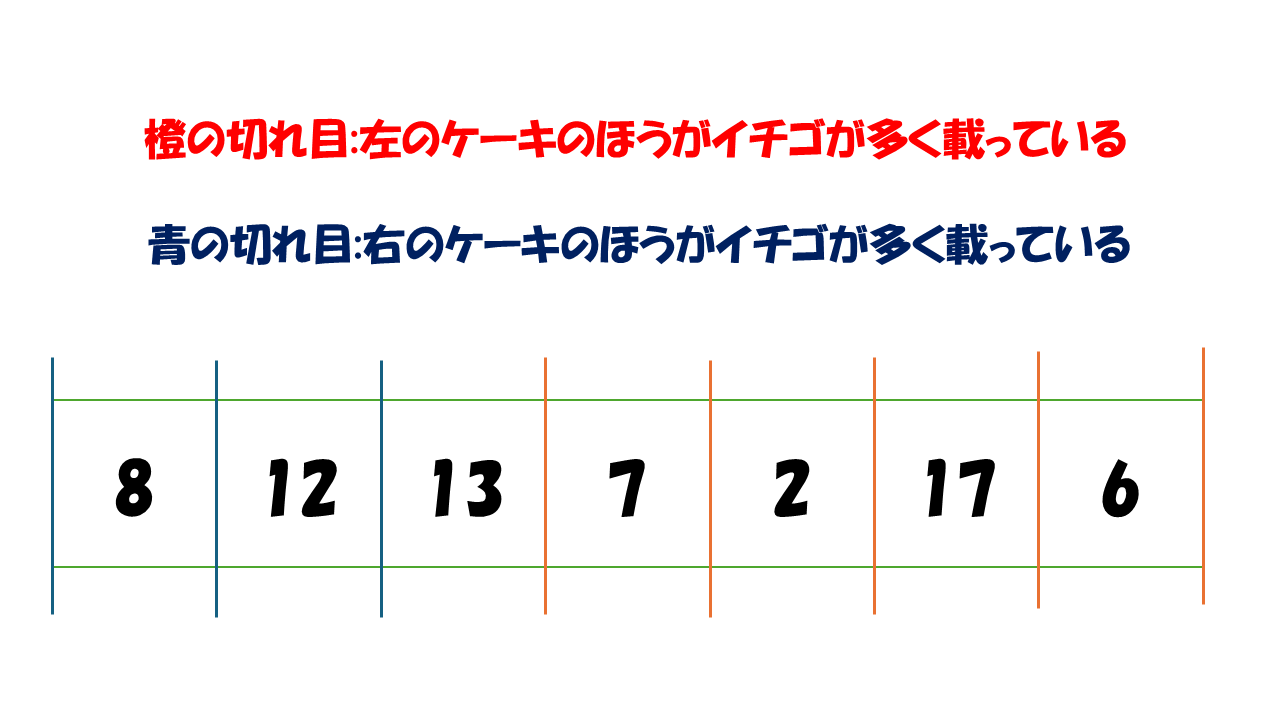
ここで、答えの候補について考えてみましょう。
左得切れ目のうち、最も左にある切れ目以外について考えてみましょう。その切れ目で切るより、左の切れ目で切った方が右のイチゴの数は減り、左のイチゴの数が増え、右のイチゴの数と左のイチゴの数の差は小さくなります。このことより、橙の切れ目のうち、最も左にある切れ目のみが答えの候補であることがわかります。
同様に、右得切れ目についても、同様のことが言え、最も右の切れ目のみが答えの候補となります。
このことから、右得切れ目と左得切れ目の入れ替わりのタイミングをもとめ、その入れ替わりのタイミングにある切れ目のみを調べればよいことがわかります。
このような入れ替わりのタイミングは、それぞれの k でどのように求めるかについて考えていきます。
単調性があるので、二分探索で求めることが出来ます。
また、別解として、右得切れ目と左得切れ目の入れ替わりのタイミングが k = 0, 1, ... と増えていくたびにどのように変わっていくかを考えていくことでも解くことが出来ます。
左からケーキを食べていくので、同じ切れ目で切ることを考えた時に、k が大きくなるにつれ左のイチゴの数が減っていくことが変わります。それに対して、右のイチゴの数は変わりません。
この事実により、k が大きくなることにより右得切れ目が左得切れ目に変わることはないことがわかります。
このことと、単調性により k = 0, 1, ... と大きくなるにつれ右得切れ目と左得切れ目の入れ替わりのタイミングは右に移っていくことがわかるので、この移行を追うことにより求めることが可能です。
では、実際にやってみましょう。以下に問題を再掲します。
(問題)
N 個のセグメントに分かれている 1 次元のケーキがあり、i (1 ≦ i ≦ N) 番目のセグメントには A_i 個のイチゴが載っています。
k = 0, 1, ..., N - 2 に対して、それぞれ以下の問題の答えを求めてください。
左から k 個のセグメント分のケーキを食べてしまいました。残ったセグメントの中から切れ目を 1 つ選び、2 つのケーキに分けます。2 つのケーキに乗っているイチゴの数の差の最小値を求めてください。
- 入力される値
-
入力は以下のフォーマットで与えられます。
N
A_1 A_2 ... A_N
1 行目には 1 つの整数 N が与えられます。
2 行目には N 個の整数 A_1,A_2,...,A_N が与えられます。
入力は合計で 2 行からなり、入力値最終行の末尾に改行が 1 つ入ります。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
答えを N - 1 行で出力してください。
i (1 ≦ i ≦ N - 1) 行目には k = i - 1 のときの答えを出力してください。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
- 2 ≦ N ≦ 200000
- 1 ≦ A_i ≦ 10 ^ 9 (1 ≦ i ≦ N)
- 入力例1
-
7
8 12 13 7 2 17 6
- 出力例1
-
1
7
1
14
13
11
- 入力例2
-
5
1 1 1 1 1000
- 出力例2
-
996
997
998
999

