(問題 2) イチゴ争奪戦 step.2 C++編(paizaランク B 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
N 個のセグメントに分かれている 1 次元のケーキがあり、i (1 ≦ i ≦ N) 番目のセグメントには A_i 個のイチゴが載っています。これらのセグメントの中から切れ目を 1 つ選び、2 つのケーキに分けます。2 つのケーキに乗っているイチゴの数の差の最小値を求めてください。
(制約) 2 ≦ N ≦ 200000, 1 ≦ A_i ≦ 10 ^ 9 (1 ≦ i ≦ N)
この問題を解いてみましょう。問題 1 と同じように切れ目を全部試してみることにします。
しかし、セグメントの数が多いため、それぞれの切れ目にたいし、問題 1 のようにイチゴの数を足して求めているのではプログラムの実行時間が長くなってしまい、制限に間に合いません。
ここで、高速に左右のケーキに載っているイチゴの数を求める方法を学習していきます。2 通りの方法を紹介します。
1 つ目は、累積和をもちいる方法です。問題 1 で見てきた例をまた見ていきます。
7 個のセグメントに左からイチゴが、8 個、12 個、13 個、7 個、2 個、17 個、6 個載っている状況を考えます。
4 番目のセグメントと 5 番目のセグメントの間で切れ目を入れています。そのとき、左のケーキに載っているイチゴの数は左から 4 番目のセグメントまでの載っているイチゴの総和です。
ここで、S_i を左から i 番目のセグメントまでの載っているイチゴの総和とします。つまり、S_i = A_1 + A_2 + A_3 + ... + A_i です(S_0 は 0 とします)。S_0,S_1,...,S_N は事前に計算することが出来ます(方法は S_0 = 0 とし、i = 1, 2, ..., N の順番で S_i = S_{i-1} + A_i と計算します)。
先ほどの例でいうと S_0 = 0, S_1 = 8, S_2 = 20, S_3 = 33, S_4 = 40, S_5 = 42, S_6 = 59, S_7 = 65 です。
このとき、左側のケーキのイチゴの数は S_4 = 40 個と計算が出来ます。右側のケーキに乗っているイチゴの数は、全体(7 個のセグメントまでの載っているイチゴの総和) から左から 4 番目のセグメントまでの載っているイチゴの総和を引いたものと考えることが出来るので、S_7 - S_4 = 25 個と計算が出来ます。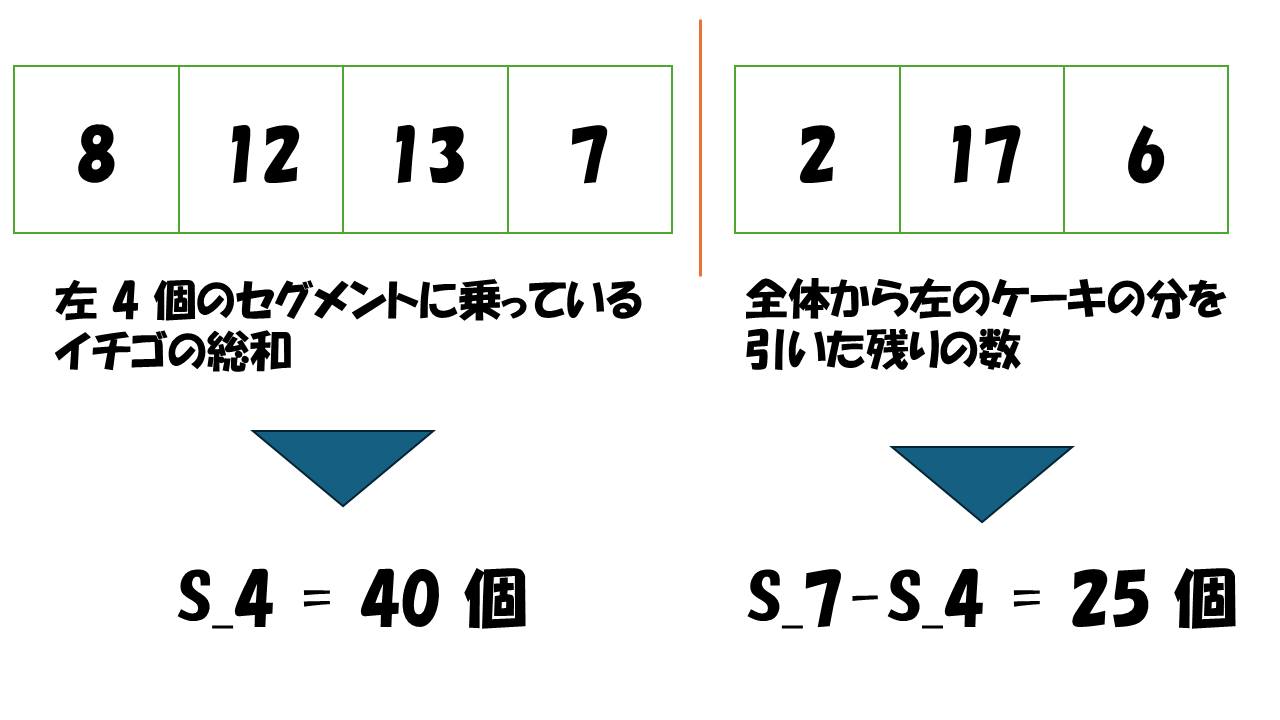
このように、事前に累積和を計算することによって、各切れ目に対し、左側と右側のケーキに載っているイチゴの数を高速に計算することが出来ます。
2 つ目は差分更新の方法です。
4 番目のセグメントと 5 番目のセグメントの間で切れ目を入れた場合と、その右隣の切れ目である 5 番目のセグメントと 6 番目のセグメントの間で切れ目を入れた場合の差分を考えます。以降、4 番目のセグメントと 5 番目のセグメントの間で切れ目を入れた場合を前者、5 番目のセグメントと 6 番目のセグメントの間で切れ目を入れた場合を後者とします。
左側のケーキについて見ていきます。前者の場合左側のケーキは左 4 個のセグメントで出来ているので、8 + 12 + 13 + 7 = 40 個と求められます。後者の場合は、左 5 個のセグメントでできているので 8 + 12 + 13 + 7 + 2 = 42 個と求められます。右側のケーキについても同様に計算が出来ます。
ここで、それぞれのケースについて差分を見ていきます。切れ目を右側にうつしたことによって、5 番目のセグメントが右側のケーキに属していたのが、左側のケーキに属すようになったことがわかります。また、それ以外はどちらに属すかについては変わっていないこともわかります。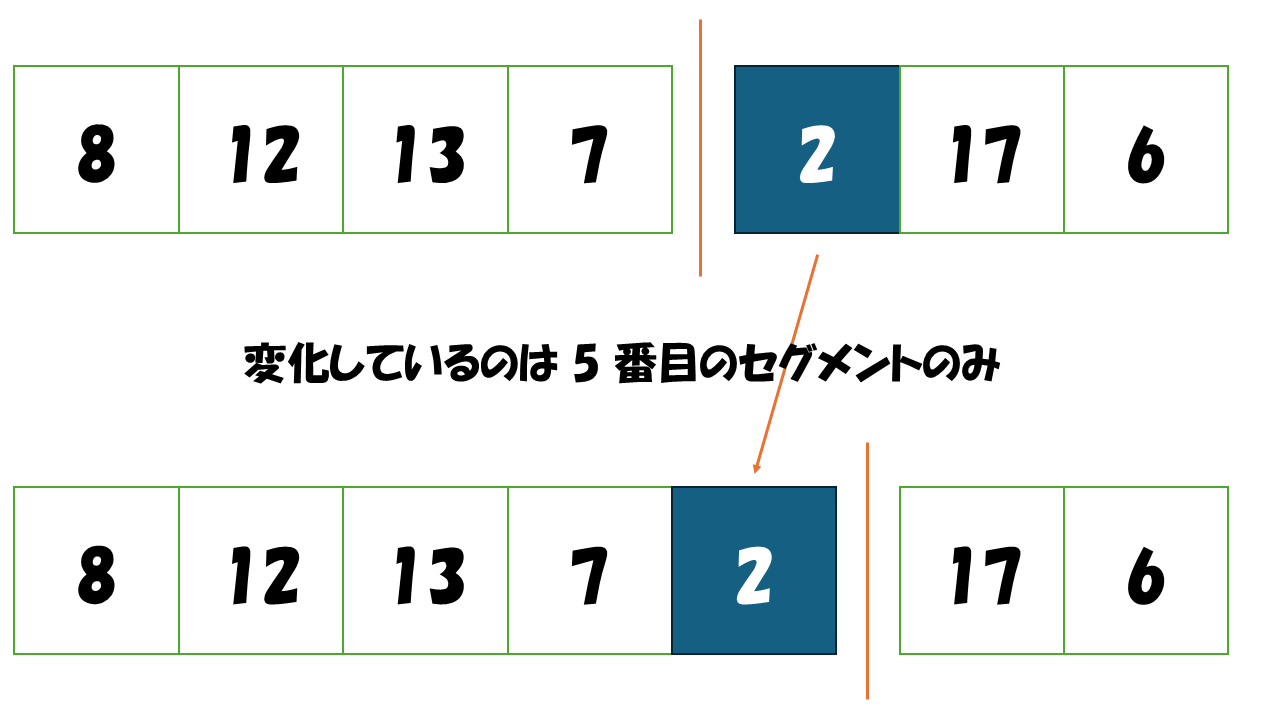
以上より、切れ目を右側にうつしたことによって、左側のケーキは 5 番目のセグメントに載っているイチゴの分だけ増え、右側のケーキは 5 番目のセグメントに載っているイチゴの分だけ減っていることがわかります。
このように、差分に注目し、一番左側の切れ目から差分を更新していくことでも、各切れ目に対し、左側と右側のケーキに載っているイチゴの数を高速に計算することが出来ます。
では、実際にやってみましょう。以下に問題を再掲します。
(問題)
N 個のセグメントに分かれている 1 次元のケーキがあり、i (1 ≦ i ≦ N) 番目のセグメントには A_i 個のイチゴが載っています。これらのセグメントの中から切れ目を 1 つ選び、2 つのケーキに分けます。2 つのケーキに乗っているイチゴの数の差の最小値を求めてください。
- 入力される値
-
入力は以下のフォーマットで与えられます。
N
A_1 A_2 ... A_N
1 行目には 1 つの整数 N が与えられます。
2 行目には N 個の整数 A_1,A_2,...,A_N が与えられます。
入力は合計で 2 行からなり、入力値最終行の末尾に改行が 1 つ入ります。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
答えを 1 行で出力してください。
最後は改行し、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
- 2 ≦ N ≦ 200000
- 1 ≦ A_i ≦ 10 ^ 9 (1 ≦ i ≦ N)
- 入力例1
-
7
8 12 13 7 2 17 6
- 出力例1
-
1
- 入力例2
-
5
1 1 1 1 1000
- 出力例2
-
996

