(問題 12) NGABCOverゲーム step.final Python3編(paizaランク S 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
3 つの変数 A, B, C がはじめすべて 0 で初期化されています。また、N 個の数字のトリオ (a_i, b_i, c_i) および確率 T_ i が与えられます。AliceさんとBobさんは変数 A, B, C に対して、以下のように行動していきます。
N 個の中から 1 つ数字のトリオ (a_i, b_i, c_i) を選ぶ。T_i % の確率で A に a_i、B に b_i、C に c_i を加算される。ただし、行動後 A が P 以下、B が Q 以下、C が R 以下にならなければならない。
Aliceさんから始め、先に A, B, C のいずれかが P, Q, R を超えてしまったほうの負けです。2 人が純粋最適戦略を行ったときにAliceさんの勝率を求めてください。
まず、(A, B, C) = (D, E, F) であり、Aliceさんが先手の状況を考えましょう。
仮に数字のトリオ (d, e, f) を選んだとします。そのとき、T % の確率で、(A, B, C) = (D + d, E + e, F + f) に、100 - T % の確率で (A, B, C) = (D, E, F) となり、AliceさんとBobさんのターンが入れ替わり、Aliceさんが後手の状態になります。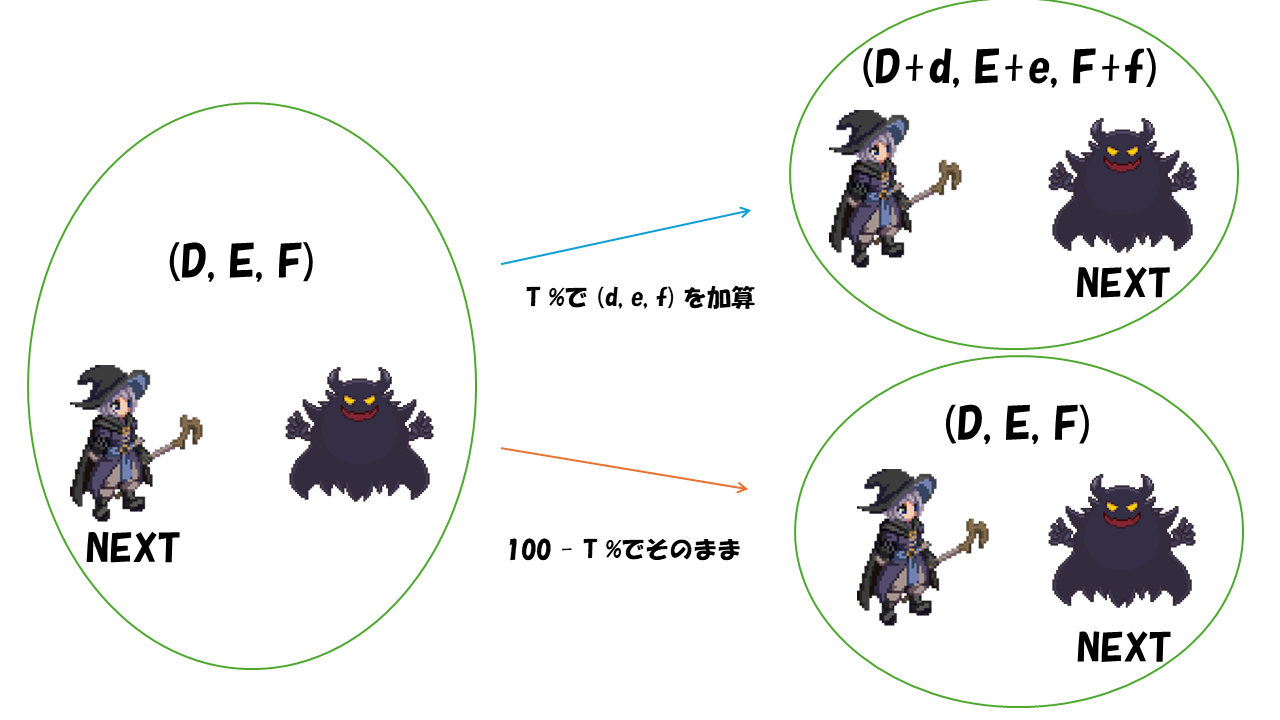
では、(A, B, C) = (D + d, E + e, F + f) の盤面の先手の勝率が X % であるときの、この手を選んだ時の (A, B, C) = (D, E, F) の盤面の先手の勝率 Y % を求めてみましょう。
T % の確率で (A, B, C) = (D + d, E + e, F + f) の盤面のときの後手になり、100 - T % の確率で (A, B, C) = (D, E, F) の盤面で後手になるので、この手を選んだ場合の勝率は 100 * ((T / 100) * ((100 - X) / 100) + ((100 - T) / 100) * ((100 - Y) / 100)) % となります。
よって、Y = 100 * ((T / 100) * ((100 - X) / 100) + ((100 - T) / 100) * ((100 - Y) / 100)) より、Y = (10000 - T * X) / (200 - T) となります。
他の手を選んだ場合にも同様のことが言えます。よって、このように勝率を求めてから勝率が最も高い手を選ぶのが純粋最適戦略となります。
Bobさんが先手であった場合も同様のことが言えます。
よって以下のDPを考えてみましょう。
DP[D][E][F] = ((A, B, C) = (D, E, F) からゲームを始めた時の先手の勝率)
まず、D が P 以下、E が Q 以下、F が R 以下のいずれかを満たしていなければ、ゲームが終了しています。このとき、この盤面に遷移させたものが負けなので、先手の勝率を 100 % としてあつかうことで、この盤面に遷移させた(後手に入れ替わった)ものの負けを表現できます。
そうでないとき、N 個の選んだ手にたいして、それぞれ勝率がわかっているならば最も先手の勝率が大きくなるような手を選ぶのは最適です。
問題 7 で扱った後退解析を行うことにより、すべての盤面に対して先手の勝率を求めることが出来ます。
問題
3 つの変数 A, B, C がはじめすべて 0 で初期化されています。また、N 個の数字のトリオ (a_i, b_i, c_i) および確率 T_ i (1 ≦ i ≦ N) が与えられます。AliceさんとBobさんは整数 A, B, C に対して、以下のように行動していきます。
Aliceさんから始め、先に A, B, C のいずれかが P, Q, R を超えてしまったほうの負けです。2 人が純粋最適戦略を行ったときにAliceさんの勝率を百分率で求めてください。
- 入力される値
-
入力は以下のフォーマットで与えられます。
N P Q R
a_1 b_1 c_1 T_1
a_2 b_2 c_2 T_2
...
a_N b_N c_N T_N
1 行目には 4 つの整数 N,P,Q,R が与えられます
i + 1 (1 ≦ i ≦ N) 行目には 4 つの整数 a_i,b_i,c_i,T_i が与えられます。
入力は合計で 1 + N 行からなり、入力値最終行の末尾に改行が 1 つ入ります。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
答えを 1 行で出力してください。
絶対誤差もしくは相対誤差が 10 ^ -4 以下であるとき正解と判定されます。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ N ≦ 10
- 1 ≦ P, Q, R ≦ 75
- 0 ≦ a_i ≦ P (1 ≦ i ≦ N)
- 0 ≦ b_i ≦ Q (1 ≦ i ≦ N)
- 0 ≦ c_i ≦ R (1 ≦ i ≦ N)
- a_i + b_i + c_i > 0 (1 ≦ i ≦ N)
- 1 ≦ T_i ≦ 100 (1 ≦ i ≦ N)
- 入力例1
-
1 3 3 3
3 3 3 50
- 出力例1
-
55.555555555555555555555555555555555555555555556
- 入力例2
-
3 75 75 74
1 0 0 47
0 1 0 59
0 0 1 77
- 出力例2
-
50.000000000000000000000000000000000000000000000

