(問題 9) サイコロ step.2 Python3編（paizaランク B 相当）

各面の出る確率が等しい N 面のダイスがあり、このダイスを最大で 2 回まで振ることができます。最終的な出目が i のとき、スコアは c_i になります。スコアの期待値を最大化するような戦略を取ったときの期待値を求めてください。

この問題について、例として一般的なサイコロを考えます。つまり、6 面サイコロでスコアは出目と同じである状況を考えます。

サイコロを 1 回までしか振ることが出来ない場合、戦略は 1 回振る戦略しかなく、スコアの期待値はすべての面に対して出る確率は 1/6 なので、(1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5 となります。

では、問題と同様に 2 回まで振れることを考えます。そのとき、戦略は 1 回でやめるか、2 回振るかのどちらかになります。

1 回目の出目が C であったときを考えます。このとき、ここでやめれば、スコアが C である確率は 100 %なので最終的なスコアの期待値は C になります。もう一回振った場合は、先ほど考えた 1 回までしか振ることが出来ない状態と同じ状態になり、期待値は 3.5 になります。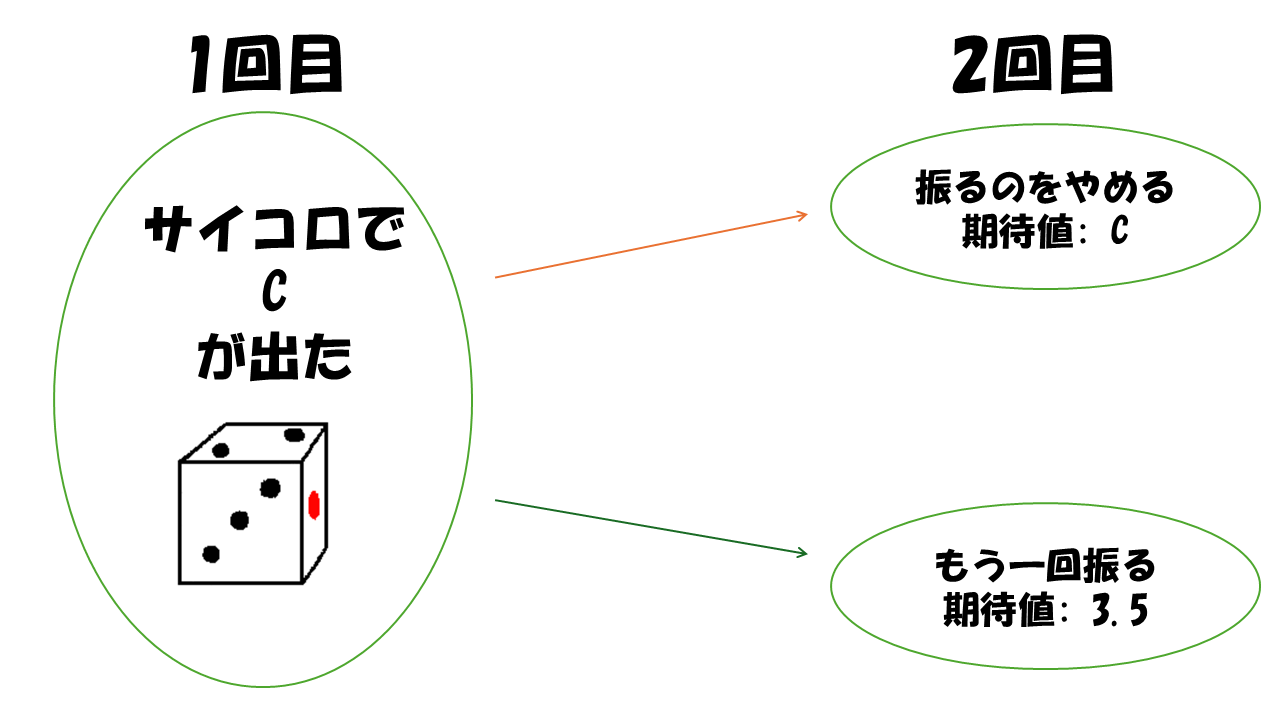



期待値は (1 回目で C が出たときの最終的なスコアの期待値) × 1/6 を C が 1 から 6 のときの総和をとったものになるので、この期待値を最大化するには、C ≧ 3.5 ならば振るのをやめ、C < 3.5 ならば、もう一回振る戦略をとることが良いことがわかります。

他の状況に関しても同様に考えることが出来ます。では、実際にやってみましょう。

問題

各面の出る確率が等しい N 面のダイスがあり、このダイスを最大で 2 回まで振ることができます。

最終的な出目が i (1 ≦ i ≦ N) のとき、スコアは C_i になります。スコアの期待値を最大化するような戦略を取ったときの期待値を求めてください。