二分探索木の実装を解くために Elixir(Beta)編(paizaランク C 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
シェア用URL:
問題
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
(はじめに)
このメニューでは、二分探索木 (Binary Search Tree, 以下 BST と表記します) の実装に取り組みます。
BST は「左の子は小さく、右の子は大きい」というルールを持つ二分木です。データの高速な検索に活用されます。
二分探索木の実装には、ノードの挿入、削除、検索、木の回転操作を実装することで理解を深めていきます。
この問題では、二分探索木の実装のために必要な前提知識を確認します。
まずは、早速問題を見てみましょう。
(問題)
N 個の整数 t1, t2, ..., tN が与えられます。
次のルールに従って木を作成し、木のノードを先行順で訪問した結果を出力してください。
・ i 番目の親の左の子は 2i 番目
・ i 番目の親の右の子は 2i+1 番目
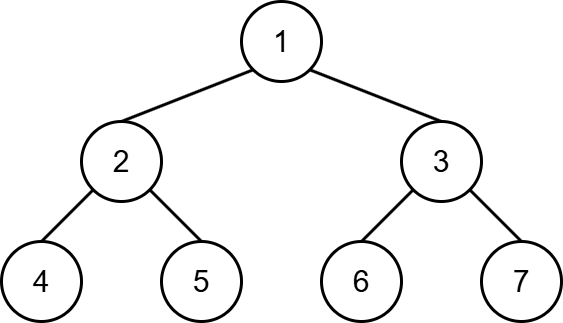
先行順について
先行順とは、根から順に左部分木、右部分木を訪問する操作方法です。
先行順は再帰を用いた以下のアルゴリズムによって実装できます。
・ 訪問したノードを出力する
・ 左の子がある場合、左の子を訪問する
・ 右の子がある場合、右の子を訪問する
・ 親ノードに戻る
- 入力される値
-
N
t1 t2 ... tN
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
作成した木の N 個のノードの要素 ti を先行順で訪問した結果を出力してください。
訪問したノードの値 ti を1行ずつ出力してください。
また、末尾に改行を入れ、余計な文字、空行を含んではいけません。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・ 3 ≦ N ≦ 20
・ 1 ≦ ti ≦ 20
- 入力例1
-
5
1 2 3 4 5
- 出力例1
-
1
2
4
5
3
- 入力例2
-
7
1 2 5 3 4 6 7
- 出力例2
-
1
2
3
4
5
6
7

