AVL木の削除実装 D(Beta)編（paizaランク A 相当）

N 個の整数 t₁, t₂, ..., t_N と M 個の整数 a₁, a₂, ..., a_N が与えられます。

次のルールに従って AVL 木を作成した後、値が a_i である M 個のノードを順番に削除し、木のノードを先行順で訪問した結果を出力してください。

全てのノードについて、以下が成り立つ

・ 入力で与えられる t1, t2, ..., tN の順に二分探索木に挿入する
・ 左の子ノードの値は現在のノードの値よりも小さい
・ 右の子ノードの値は現在のノードの値よりも大きい
・ 左右の部分木の高さの差は常に 1 以下
・ 削除するノードがあった場所には、削除するノードより大きい値を持つノードのうち、最小の値を持つノードが来る

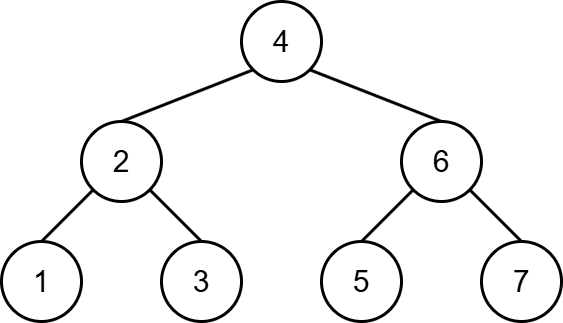
先行順について

先行順とは、根から順に左部分木、右部分木を訪問する操作方法です。

先行順は再帰を用いた以下のアルゴリズムによって実装できます。

・ 訪問したノードを出力する
・ 左の子がある場合、左の子を訪問する
・ 右の子がある場合、右の子を訪問する
・ 親ノードに戻る

木構造について

木構造は、ノード同士が関係性を持つことで作ることができます。

この問題で各ノードが持つべき情報は以下の通りです。

・ ノードの値
・ 親ノードの情報
・ 左の子ノードの情報
・ 右の子ノードの情報

AVL 木について

AVL 木は二分探索木のうちの 1 種類です。

これまでの二分探索木の特徴に加えて、全てのノードが持つ左右の部分木は高さの差が 1 以下を保ち続けるという特徴があります。

AVL 木は以下のアルゴリズムによって実装できます。

・ 二分探索木のアルゴリズムに従ってノードを木に挿入する
・ 挿入した葉から根までノードを遡って以下の操作を行う
    ・ 現在のノードの左右部分木の高さの差が 2 以上の場合
        ・ 回転操作を用いて左右部分木の高さを 1 以下にする
    ・ 1 つ親のノードに移る