(はじめに)

問題 3 にてBITの構築を行ってきました。

続いて、問題 4,5 にて一点加算を高速に処理する方法をやっていきます。

class BIT():

    def cnt2(self, I): #2で何回割れるか計算する
        k = 0
        while I % 2 == 0:
            k += 1
            I = I // 2
        return k

    def __init__(self, n, A): #BITの作成
        self.Tree = [0]* (n + 1) #0で初期化
        self.n = n
        for i in range(1, n + 1):
            k=self.cnt2(i)
            for j in range(i - 2 ** k, i): #インデックス注意
                self.Tree[i] += A[j]

    def add(self, id, x): #A[id]にxを足す作業
        #問題 4,5 で実装

    def sum(self, id): #A[id] までの累積和を計算
        #問題 6,7 で実装

(BITの一点更新について)

まず、問題 3 で扱ったBITの木構造について再掲します。



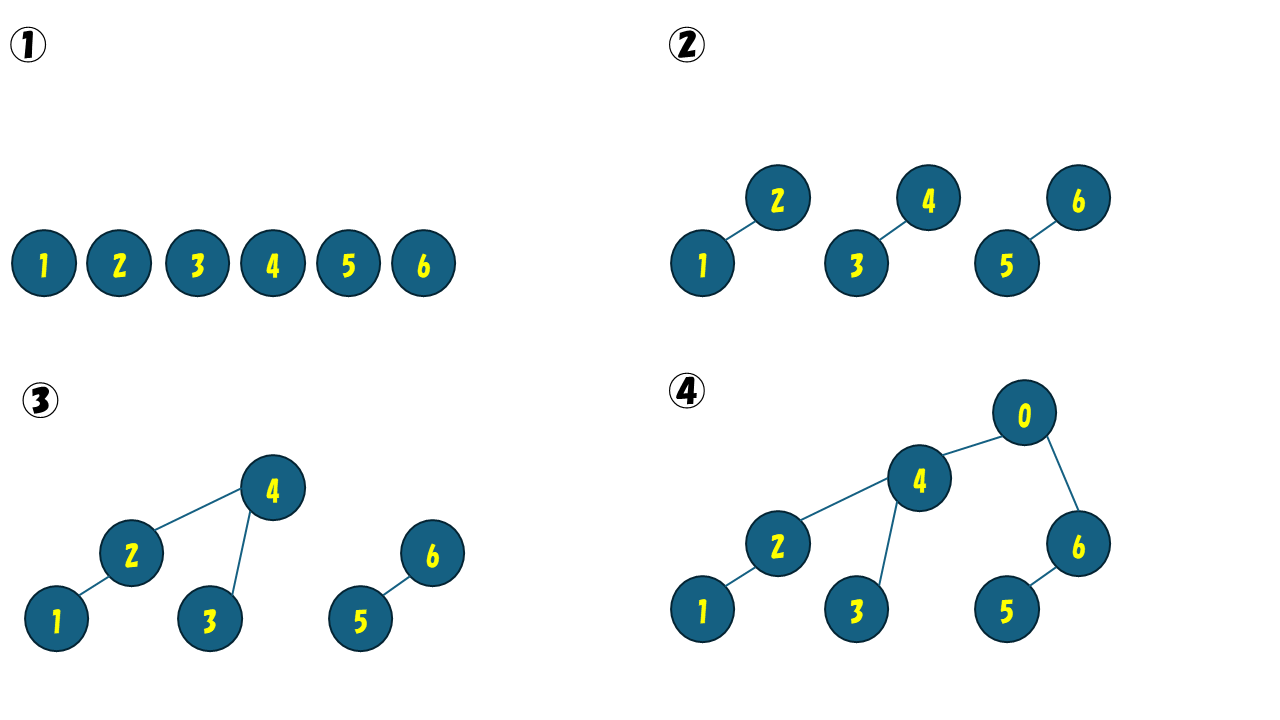
上記の図では省略されていますが、ペアになった時に親になる BIT_j に BIT_i を足し合わせる処理を行っています。

例えば、頂点 1 に格納されていた数 BIT_1 = A_1 は親である頂点 2 に足しあわされています。

そして、BIT_2 = A_1 + A_2 が格納されている頂点 2 は親の頂点 4 にも足しあわされています。

つまり、頂点 1 に格納されている数はその親の頂点 2 に影響を及ぼし、さらにその親の頂点 4 にも影響を及ぼしています。

つまり、A_1 を一点加算で更新するとき、影響を及ぼした頂点 2,4 も更新する必要があります。

また、他の頂点には影響を及ぼしていないため、更新する必要はありません。

つまり、A_1 を更新するとき、頂点 0 (根)と頂点 1 の最短パス上の頂点を更新すればよいことがわかります。

他の頂点、また、他のBITについても同様です。

A_i を更新するときには頂点 i と根の最短パス上の頂点に対応するBITの要素を更新すれば良いことがわかります。

この処理は根にたどり着くまで親に移動することで処理することが可能です。

では親の頂点はどうやって計算すればいいかについて、行っていきます。

それぞれの段の処理で一段上に行くのは、ペアで後ろになった頂点、つまり、前から見た時偶数番目にある頂点です。

最初は 1,2,3,... と並んでいるので、2 段目に行くのは 2,4,6,... つまり、頂点番号が偶数であることがわかります。

3 段目に行く頂点も同様に、偶数番目である 4,8,12,... つまり、頂点番号が 2 ^ 2 の倍数であることがわかります。

これを繰り返すと t 段目に行く頂点は、2 ^ (t - 1) の倍数であることがわかります。

親が確定するのは、特定の段に残されたときでした。では、t 段目に残される頂点はどのようなものでしょうか。

t 段目に残される頂点は「t 段目には行くことが出来たが、t + 1 段目には行くことが出来なかった。」、つまり、「頂点番号が 2 ^ (t - 1) の倍数ではあるが、2 ^ t の倍数ではない」頂点であることがわかります。

t 段目に残された頂点の親は、その時ペアになった頂点、つまり、その頂点の 1 個後ろの頂点です。

t 段目に行く頂点は 2 ^ (t - 1) の倍数であったため、頂点 i の親は i + 2 ^ (t - 1) (i は 2 ^ (t - 1) の倍数だが、2 ^ t の倍数ではない) と計算することが出来ます。

例を挙げると、頂点 5 の親は、2 ^ 0 の倍数だが 2 ^ 1 の倍数ではないため、頂点 5 + 2 ^ 0 = 6 です。

ただし、親の頂点番号の計算結果が n を超えた場合は 0 となります。

以上のことをまとめると、頂点 i (1 ≦ i ≦ n) の親は i を 2 で k 回まで割ることが出来たとすると、i + 2 ^ k で計算することが出来ます。(存在しなければ 0)

では、頂点 i と根の最短パス上の頂点を計算してみましょう。

(問題)

Q 個のクエリが与えられます。順番に処理してください。i (1 ≦ i ≦ Q) 番目のクエリは以下の通りです。

長さ n_i の配列に対して問題 3 の方法で構築したBITの木構造を考える。頂点 I_i と根(頂点 0 とする)の最短パス上の頂点を頂点 I_i との距離が近い順に出力する。