(BITの構築について)

では、いよいよBITにとりかかっていきます。

まず、BIT(Binary Indexed Tree)とは、配列の要素に値を加算するクエリ (一点加算) と、配列の区間の総和を求めるクエリ（区間総和）を高速に処理することのできるデータ構造です。

どのように管理しているのか見てみましょう。

長さ n の配列 A = (A_1,A_2,...,A_n) に対して、BIT = (BIT_0,BIT_1,BIT_2,...,BIT_n) を以下のように定義します。

BIT_0 = 0

1 ≦ i ≦ n において、i を 2 で割ることが出来る最大回数を k とおく。そのとき、BIT_i = A_{i - 2 ^ k + 1} + A_{i - 2 ^ k + 2} + ... + A_i (つまり、A_i から前 2 ^ k 個の和)

たとえば、BIT_6 = A_5 + A_6, BIT_9 = A_9, BIT_12 = A_9 + A_10 + A_11 + A_12 です。A = (1, 5, 7, 9, 8, 6) とすると、BIT = (0, 1, 6, 7, 22, 8, 14) です。

このデータ構造はfor文の二重ループで実装することが出来ます。

具体的にはそれぞれの i に対し、k を求め、その分戻って加算を行えば構築が出来ます。

ぱっと見では O (n ^ 2) に見えますが、計算量について考えていきます。小数点以下切り捨てを意味する記号としてfloor()を使います。

まず、それぞれの k (0 ≦ k) に対し、何個の i が該当するか考えていきます。

1 ≦ i ≦ n なので、k が log_2(n) を上回っている場合該当する i は 0 個です。

以降 K を floor(log_2(n)) とします。

k = K となる i の個数は i が 2 ^ K の倍数となっていて、2 ^ {K + 1} の倍数となっていない i の個数なので、該当する i は floor(n / 2 ^ K) 個です。

同様に考えると、k = t となる i の個数は i が 2 ^ t の倍数となっていて、2 ^ {t + 1} の倍数となっていない i の個数なので、該当する i は floor(n / 2 ^ t) - floor(n / 2 ^ {t + 1}) 個です。

以上のように考えると 2 個目のfor文の範囲が 2 ^ k となるものは floor(n / 2 ^ k) - floor(n / 2 ^ {k + 1}) 個です。

つまり、それぞれの k に対して、for文の範囲が 2 ^ k となるものの計算回数は 2 ^ k × (floor(n / 2 ^ k) - floor(n / 2 ^ {k + 1})) で O(n) となります。

よって、0 ≦ k ≦ K なので、全体で O(nK) = O(n log(n)) となります。

簡単に言うと、二重ループであるが n = 1000000 だとしても高速に構築をすることができます。

今後のために木の構造がどうなっているかを見ていきます。

次のように木として構築できます。

最下段に全要素を順番通りに並べる。最上段にある頂点が 1 になるまで最上段に対して以下を繰り返す。

前から 2 つずつ見ていき、そのペアの中で後ろにある頂点に前にある頂点のものを足し、後ろの頂点を一段上げ、前にある頂点の親にする。

最後にダミーの頂点(根)を用意し、親が未確定の頂点の親にする。

以下が n = 6 のときの例です。黄色が頂点番号です。



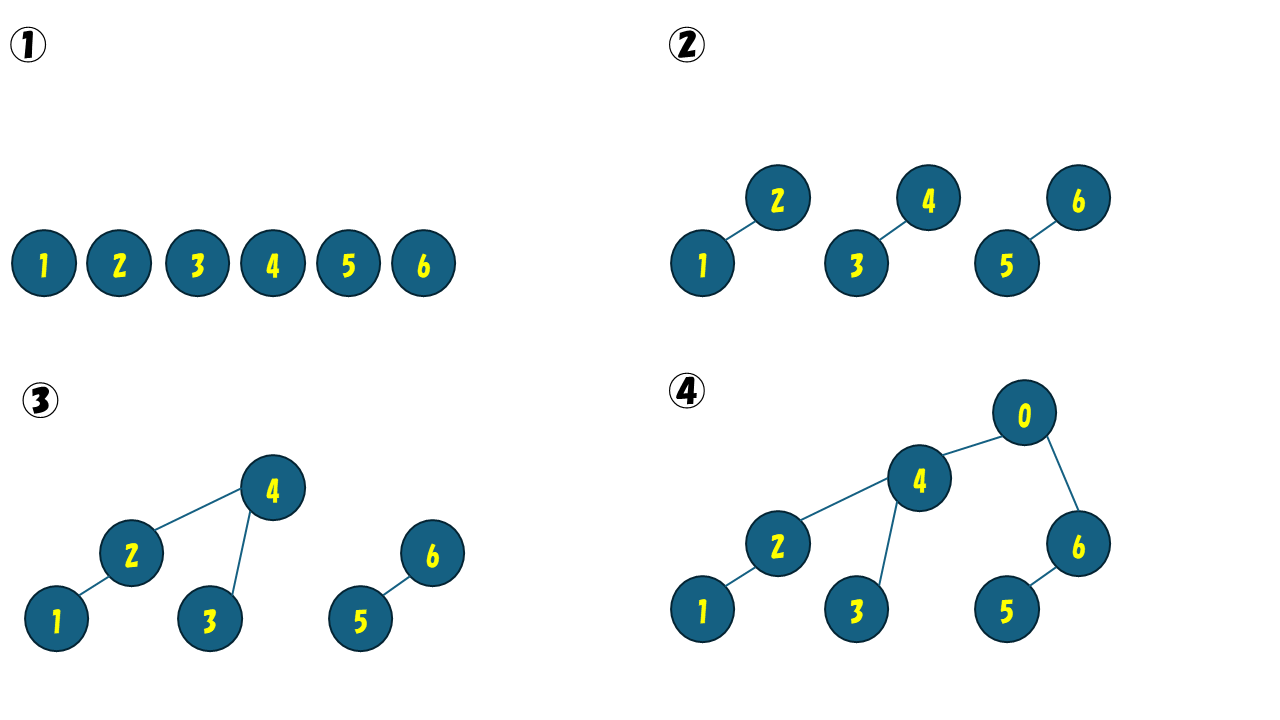
まず最下段では (1,2),(3,4),(5,6) がペアになり、2,4,6 が上の段に行きます。

次の段では (2,4) とペアになり、4 が上の段に行きます。

最上位段が 1 つになったので新たな頂点 (図では頂点 0) を追加し、まだ親が確定してない 4,6 とそれぞれ辺を張ります。

構築については以上なので、実際にやってみましょう。

(問題)

長さ n の配列 A = (A_1, A_2, ... ,A_n) が与えられます。上記の方法で配列BITを構築してください。