BITの前提知識 2 : 木について C編(paizaランク C 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
シェア用URL:
ツイートする
問題
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
(木について)
次に、木について復習していきます。
木とは、連結成分が 1 つであり、閉路を持たないグラフのことです。
そのため、木の辺の数は (頂点の数)-1 本です。
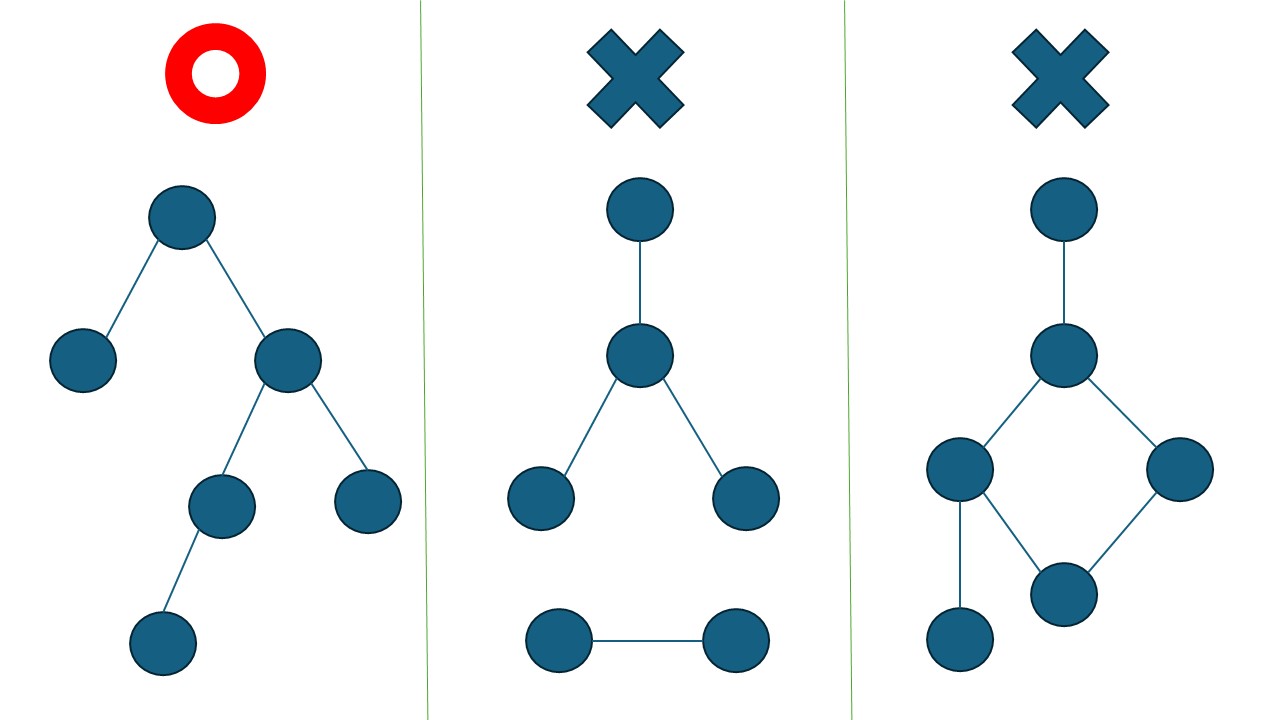
下の例でいうと、1 番左のグラフは連結成分が 1 であり、閉路を持っていないので木です。しかし、真ん中のグラフは連結成分が 2 であり、右のグラフは閉路を持っているため木ではありません。
木には、さまざまな管理方法があります。今回は隣接行列についてやっていきましょう。頂点数を N とし、頂点の番号は順に 1,2,...,N と振られているものとします。
隣接行列 (A とする) とは、N × N 行列でグラフを表したものになり 頂点 i から頂点 j に辺が張られているときには A の上から i 行目、左から j 行目の要素 (A_{i,j} とする)が 1 であり、そうでないときには、0 となっています。無向グラフの場合には A_{i,j} = A_{j,i} が必ず成り立ちます。
隣接行列は二次元配列で管理することが出来ます。実際にやってみましょう。今回の木は無向グラフなため、先ほどの性質が成り立ちます。
(問題)
N 頂点の木が与えられます。i (1 ≦ i ≦ N - 1) 番目の辺は頂点 a_i と頂点 b_i を結んでいます。
隣接行列を出力してください。
- 入力される値
-
入力は以下のフォーマットで与えられます。
N
a_1 b_1
a_2 b_2
a_3 b_3
...
a_{N-1} b_{N-1}- 1 行目には 1 つの整数 N が与えられます。
- 1 + i (1 ≦ i ≦ N - 1) 行目には 2 つの整数 a_i,b_i が与えられます。
- 入力は合計 N 行からなり、入力値最終行の末尾に改行を 1 つ含みます。
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
答えを N 行で出力してください。
i (1 ≦ i ≦ N) 行目では、隣接行列の上から i 行目を半角スペース区切りにして出力してください。
- 条件
-
すべてのテストケースについて以下の条件を満たします。
- 2 ≦ N ≦ 2000
- 1 ≦ a_i,b_i ≦ N (1 ≦ i ≦ N - 1)
- a_i ≠ b_i (1 ≦ i ≦ N - 1)
- i ≠ j なら (a_i, b_i) ≠ (a_j, b_j) かつ (a_i, b_i) ≠ (b_j, a_j)
- 与えられるグラフは木である
- 入力例1
-
6
1 2
1 3
3 4
4 5
3 6
- 出力例1
-
0 1 1 0 0 0
1 0 0 0 0 0
1 0 0 1 0 1
0 0 1 0 1 0
0 0 0 1 0 0
0 0 1 0 0 0
- 入力例2
-
2
2 1
- 出力例2
-
0 1
1 0

