(はじめに)

この問題集ではBinary Indexed Tree(以降BIT)についてやっていきます。

まずはじめに、BITを使う上での前提知識である 2 進数や木について復習していきます。

そのあとBITの構築、更新、区間クエリの計算という順序で作成した後、最後にBITを使って問題を解く流れになります。

以下にPythonコードを載せます。今後の問題でこのコードを完成させることを目標にしていきます。

class BIT():
    def __init__(self, n, A):
        #BITの構築
        #問題 3 で実装

    def add(self, id, x): #A[id]にxを足す作業
        #問題 4,5 で実装

    def sum(self, id): #A[id] までの累積和を計算
        #問題 6,7 で実装

(2 進数について)

一般的に社会で使われている数は 10 進数ですが、コンピュータなどで使われている数は 2 進数となります。

10 進数は 0,1,2,3,4,5,6,7,8,9 の 10 個の数字の組み合わせで数が表現されている一方、2 進数は 0,1 のみで表現されています。

しかし、基本的な考え方は同じです。

まず、10 進数で考えます。357 について、一番右の 1 (= 10 ^ 0) の位は 7、左隣の 10 (= 10 ^ 1) の位は 5、さらに左隣の 100 (= 10 ^ 2) の位は 3 となっています。これは 10 ^ 2 が 3 個、 10 ^ 1 が 5 個、10 ^ 0 が 7 個で構成されていることを意味します。

2 進数も同じです。1011(2) では、一番右の 1 (= 2 ^ 0) の位は 1。左隣の 2 (= 2 ^ 1) の位は 1、さらに左隣の 4 (= 2 ^ 2) の位は 0、一番左の 8 (= 2 ^ 3) の位は 1 となっています。 同様にこれは 2 ^ 3 が 1 個、 2 ^ 2 が 0 個、2 ^ 1 が 1 個、2 ^ 0 が 1 個で構成されていることを意味します。



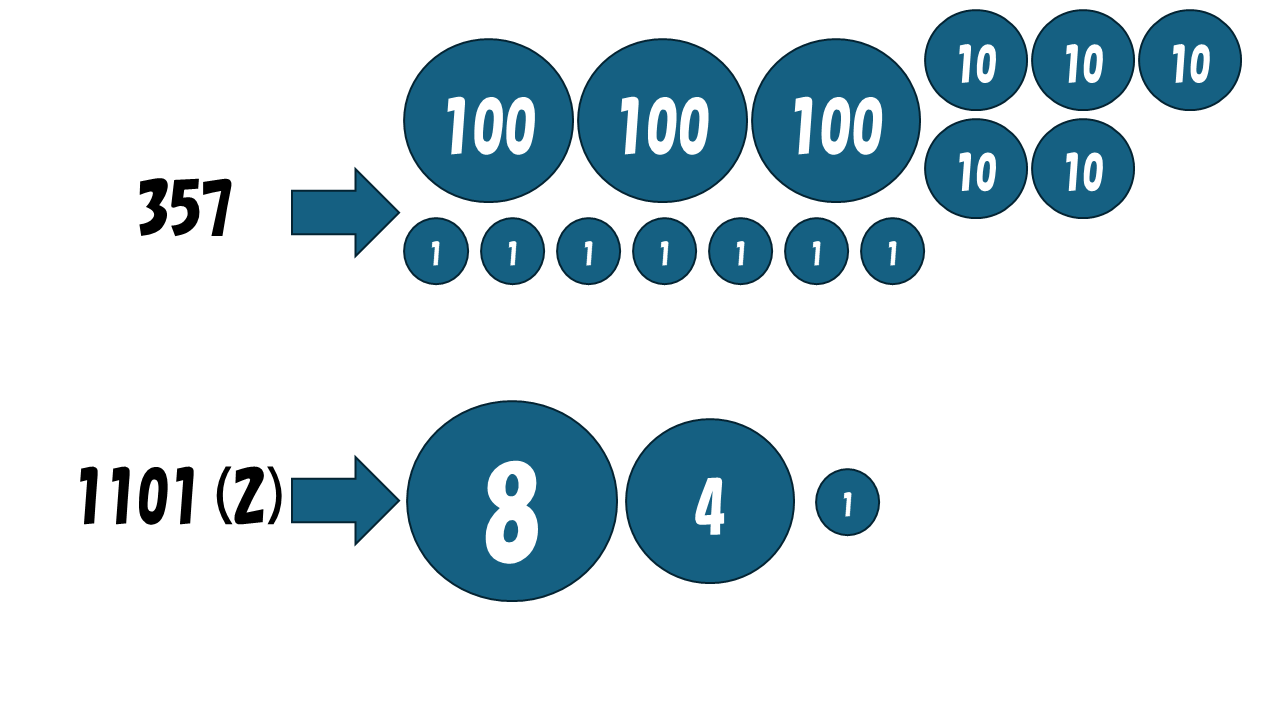
なので 1011(2) は 10 進数では 13 です。また正の数を 2 進数になおすには、下から見ていき、商が 0 になるまで、2 で 割った余りを記録し、2 で割る(切り捨て)ということを繰り返し、記録した順とは逆に読んでいけば良いです。

例えば、6 を 2 進数になおすとすると 6 ÷ 2 = 3 ... 0, 3 ÷ 2 = 1 ... 1, 1 ÷ 2 = 0 ... 1 で逆から読んで 110(2) となります。

では、ここでは 10 進数を 2 進数になおしてみましょう。

(問題)

T 個の整数 X_1,X_2,...,X_T が 10 進数で与えられるので、2 進数になおしてください。ただし先頭に余計な 0 は付けないでください。