フラクタルな根付き木 Bash(Beta)編(paizaランク A 相当)
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう!
 下記の問題をプログラミングしてみよう!
下記の問題をプログラミングしてみよう!
以下のような、フラクタルな根付き木が与えられます。
・ 基本的には通常の根付き木と同じ
・ 親から子に向けて辺が張られている
・ 一部の葉の頂点が、「自身の木を表す頂点」になっている
・ 根の番号は 1 である
例を見てみましょう。この例では、頂点 2 が「自身の木を表す頂点」になっています。左にある展開前の木を実際に展開したものが右の図のようになります。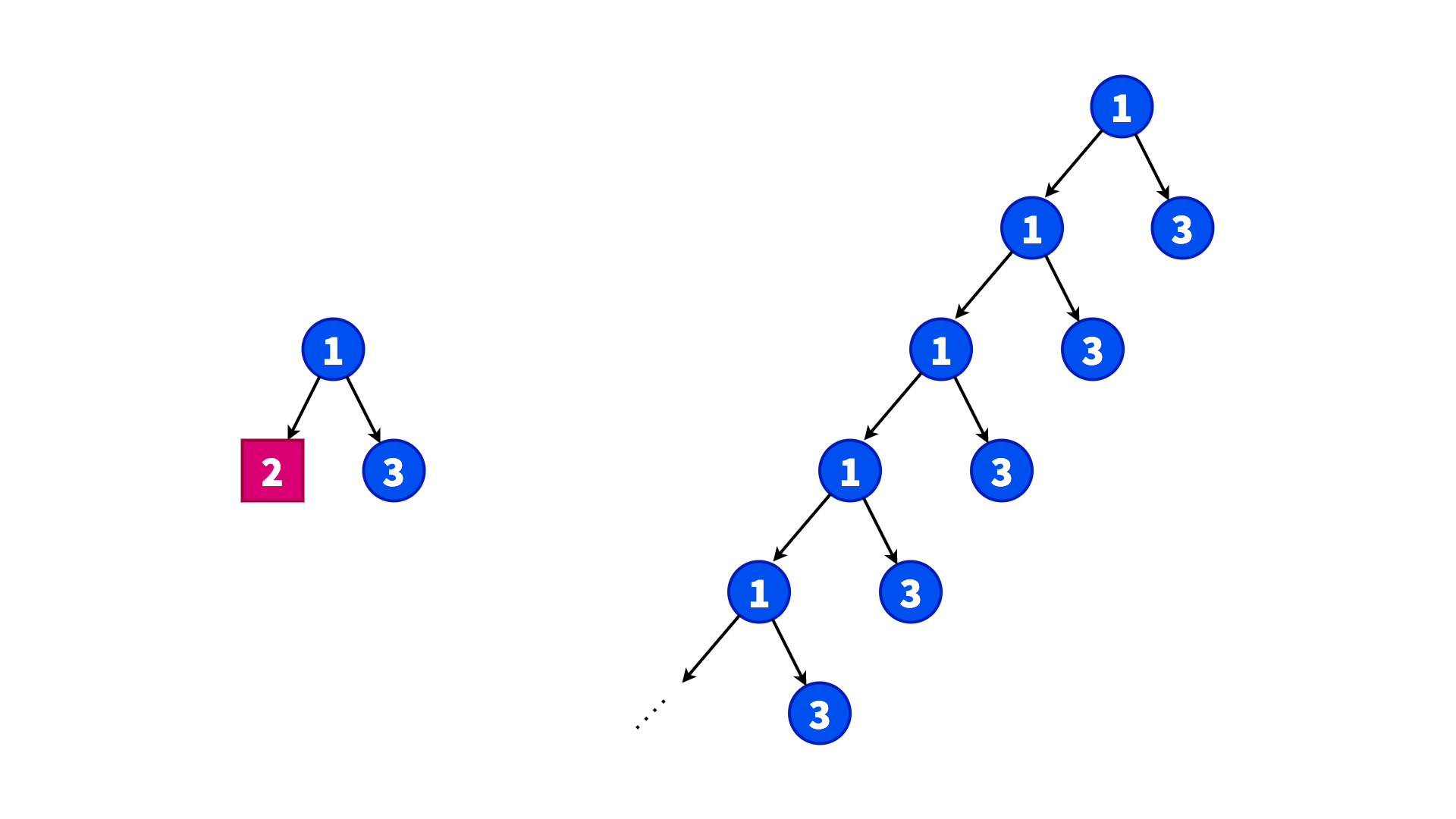
整数の組 x, y が k 個与えられるので、それぞれについて、展開した後の木における、頂点 x から 頂点 y までの最短距離を求めてください。ただし、同じ整数の頂点が複数存在する場合は、あらゆる頂点を考えた上での最短距離を求めるものとします。また、展開前の木において、頂点 x は頂点 y の祖先でないことが保証されます。
なお、頂点 a が頂点 b の祖先であるとは、頂点 b から親をたどっていったときに、頂点 a に到達できることを指します。
また、ここにおける最短距離とは、グラフ理論における距離 (最短経路の辺の数) を指します。
- 入力される値
-
n k
p_2 c_2
...
p_n c_n
x_1 y_1
x_2 y_2
...
x_k y_k
・ 1 行目に、頂点の個数を表す整数 n, 頂点の組の個数を表す整数 k が与えられます。
・ 続く n - 1 行では、i 番目の頂点の親の番号を表す整数 p_i, i 番目の頂点が自身の木を表す頂点かどうかを表す整数 c_i が半角スペース区切りで与えられます。(2 ≦ i ≦ n)
・ 続く k 行では、頂点の番号の組 x_j, y_j が半角スペース区切りで与えられます。(1 ≦ j ≦ k)
入力値最終行の末尾に改行が1つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
合計 k 行出力してください。
i 行目には、x_i から y_i にたどりつくことができるならその最短距離を、そうでなければ -1 を出力してください。
また、末尾に改行を入れ、余計な文字を含んではいけません。
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・ 入力はすべて整数
・ 2 ≦ n ≦ 200,000 = 2 × 10^5
・ 1 ≦ k ≦ 200,000 = 2 × 10^5
・ 1 ≦ p_i < i
・ c_i = 0 (通常の頂点) または c_i = 1 (自身の木を表す頂点)
・ c_i = 1 ならば頂点 i は葉である
・ 頂点 1 は通常の頂点である
・ 1 ≦ x_i, y_i ≦ n
・ x_i ≠ y_i
・ x_i は y_i の祖先でない
・ c_{x_i} = c_{y_i} = 0
- 入力例1
-
3 1
1 1
1 0
3 1
- 出力例1
-
-1
- 入力例2
-
4 1
1 0
2 1
1 0
2 1
- 出力例2
-
1

