有向グラフの隣接行列と隣接リスト C編（paizaランク B 相当）
問題にチャレンジして、ユーザー同士で解答を教え合ったり、コードを公開してみよう！
下記の問題をプログラミングしてみよう！
以下の図のような、ノード（頂点）と向きのあるエッジ（辺）の集合を有向グラフといいます。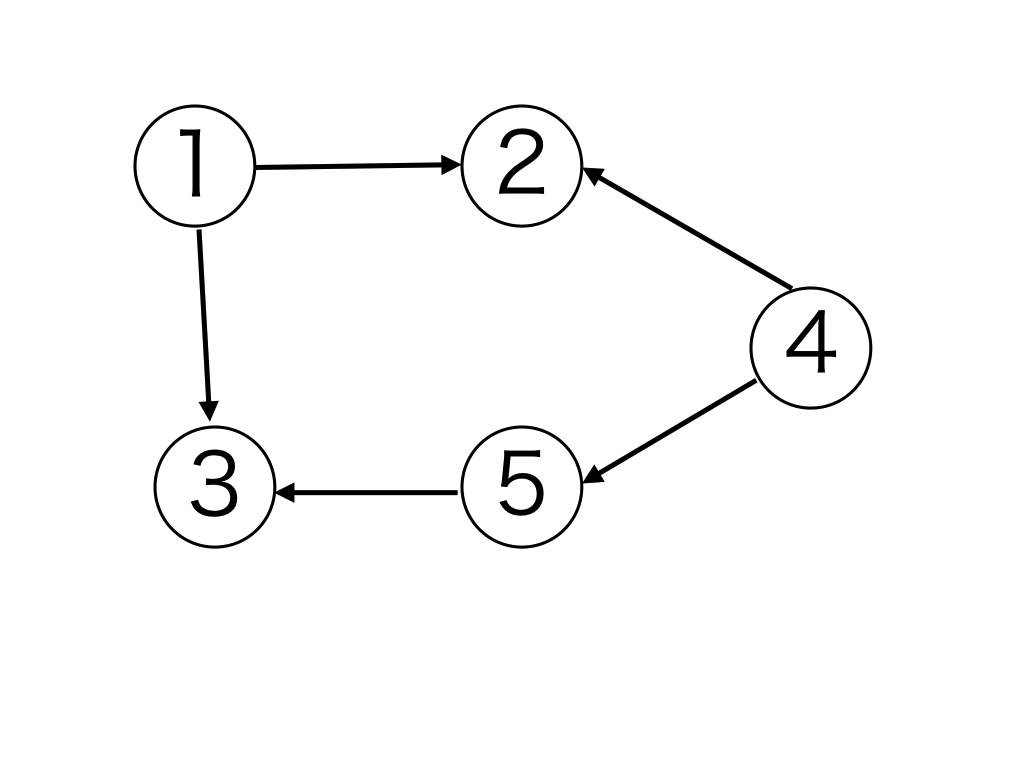
頂点の数が N であるような有向グラフにおいて、 N × N の配列 g を考えます。
i 番目の頂点から j 番目の頂点に向かう辺があるとき、 g[i-1][j-1] = 1 , ないとき、 g[i-1][j-1] = 0
であるような配列をそのグラフの隣接行列といいます。
頂点の数が N であるような有向グラフにおいて、 N 個の配列を持つ 2 次元配列 g を考えます。
i 番目の頂点から j 番目の頂点に向かう辺があるとき、 g の i-1 番目の配列に j-1 を追加します。
この操作を繰り返してできる 2 次元配列 g を隣接リストといいます。
グラフの頂点・辺についての情報が与えられるので、このグラフの隣接行列と隣接リストを出力してください。
なお、このグラフには、多重辺や自己ループはないものとします。
- 入力される値
-
N M
a_1 b_1
...
a_M b_M
・ 1 行目には、頂点の数 N と、辺の数 M が与えられます。
・ 続く M 行では、各辺の始点 a_i と、終点 b_i が与えられます。(1 ≦ i ≦ M)
入力値最終行の末尾に改行が１つ入ります。
文字列は標準入力から渡されます。 標準入力からの値取得方法はこちらをご確認ください
- 期待する出力
2×N 行の出力
・ まず、隣接行列 g を N 行で出力してください。
・ 次に、隣接リスト h を N 行で出力してください。
・ 隣接リストの各行の頂点番号は昇順にソートしてください。
・ 頂点 i (1 ≦ i ≦ N) に隣接している頂点がない場合は改行のみ出力してください。g[0][0]...g[0][N-1]
...
g[N-1][0]...g[N-1][N-1]
h[0][0]h[0][1]...
...
h[N-1][0]h[N-1][1]...
- 条件
-
すべてのテストケースにおいて、以下の条件をみたします。
・ 1 ≦ N ≦ 100
・ 1 ≦ M ≦ N × (N - 1) / 2
・ 1 ≦ a_i,b_i ≦ N
- 入力例1
-
2 1
2 1
- 出力例1
-
00
10
0
- 入力例2
-
10 10
2 4
5 7
4 7
9 10
10 2
1 5
1 8
4 5
7 8
1 10
- 出力例2
-
0000100101
0001000000
0000000000
0000101000
0000001000
0000000000
0000000100
0000000000
0000000001
0100000000
479
3
46
6
7
9
1
